
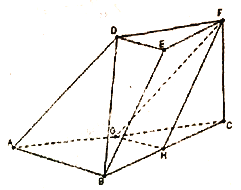
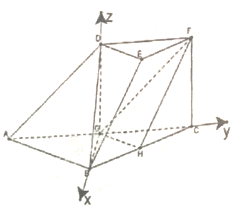
【题目】如图,在三棱台![]() 中,
中, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成角(锐角)的大小.
所成角(锐角)的大小.
【答案】(1)见解析(2)![]() .
.
【解析】试题分析:(1)根据AB=2DE可得到BC=2EF,从而可以得出四边形EFHB为平行四边形,从而得到BE∥HF,便有BE∥平面FGH,再证明DE∥平面FGH,从而得到平面BDE∥平面FGH,从而BD∥平面FGH;
(2)连接HE,根据条件能够说明HC,HG,HE三直线两两垂直,从而分别以这三直线为x,y,z轴,建立空间直角坐标系,利用两平面的法向量求解二面角的大小.
试题解析:
由![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,
,
又![]() ,
, ![]() ,则
,则![]() ,于是
,于是![]() 两两垂直,
两两垂直,
以点![]() 为坐标原点,
为坐标原点, ![]() 所在的直线分别为
所在的直线分别为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
设![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 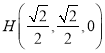
(1)证明:连接![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() .在三棱台
.在三棱台![]() 中,
中, ![]() ,则
,则![]() ,
,
而![]() 是
是![]() 的中点,
的中点, ![]() ,则
,则![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
![]() 是
是![]() 的中点,
的中点, ![]() .
.
又在![]() 中,
中, ![]() 是
是![]() 的中点,则
的中点,则![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
故![]() 平面
平面![]()
(2)平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则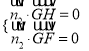 ,即
,即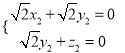 ,
,
取![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
![]() ,故平面
,故平面![]() 与平面
与平面![]() 所成角(锐角)的大小为
所成角(锐角)的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知条件p:A={x|x2﹣2mx+m2﹣4≤0,x∈R,m∈R},条件q:B={x|x2﹣2x﹣3≤0,x∈R}.
(1)若A∩B={x|0≤x≤3},求实数m的值;
(2)若q是¬p的充分条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:(a-1)x+y+b=0,l2:ax+by-4=0,求满足下列条件的a,b的值.
(1)l1⊥l2,且l1过点(1,1);
(2)l1∥l2,且l2在第一象限内与两坐标轴围成的三角形的面积为2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,
, ![]() 为椭圆
为椭圆![]() 上的任意一点(不含长轴端点),且
上的任意一点(不含长轴端点),且![]() 面积的最大值为1.
面积的最大值为1.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且线段
,且线段![]() 的中点不在圆
的中点不在圆![]() 内,求
内,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了![]() 人,回答问题计结果如下图表所示:
人,回答问题计结果如下图表所示:

(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,等比数列
,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)21或
;(2)21或![]() .
.
【解析】试题分析:(1)设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() ,由已知条件求出
,由已知条件求出![]() ,再写出通项公式;(2)由
,再写出通项公式;(2)由![]() ,求出
,求出![]() 的值,再求出
的值,再求出![]() 的值,求出
的值,求出![]() 。
。
试题解析:设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() 有
有![]() ,即
,即![]() .
.
(1)∵![]() ,结合
,结合![]() 得
得![]() ,
,
∴![]() .
.
(2)∵![]() ,解得
,解得![]() 或3,
或3,
当![]() 时,
时,![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() ,此时
,此时![]() .
.
【题型】解答题
【结束】
20
【题目】如图,已知直线与抛物线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,
, ![]() 交
交![]() 于
于![]() ,且点
,且点![]() 的坐标为
的坐标为![]() .
.
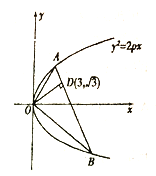
(1)求![]() 的值;
的值;
(2)若![]() 为抛物线的焦点,
为抛物线的焦点, ![]() 为抛物线上任一点,求
为抛物线上任一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式xex﹣2ax+a<0的非空解集中无整数解,则实数a的取值范围是( )
A.[ ![]() ,
, ![]() )
)
B.[ ![]() ,
, ![]() )
)
C.[ ![]() ,e]
,e]
D.[ ![]() ,e]
,e]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com