
【题目】(2017高考新课标Ⅲ,理19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)利用题意证得二面角的平面角为90°,则可得到面面垂直;
(2)利用题意求得两个半平面的法向量,然后利用二面角的夹角公式可求得二面角D–AE–C的余弦值为![]() .
.
试题解析:(1)由题设可得,![]() ,从而
,从而![]() .
.
又![]() 是直角三角形,所以
是直角三角形,所以![]() .
.
取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO.
又由于![]() 是正三角形,故
是正三角形,故![]() .
.
所以![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() .
.
又![]() ,所以
,所以![]() ,
,
故![]() .
.
所以平面ACD⊥平面ABC.
(2)由题设及(1)知,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,
轴正方向,![]() 为单位长,建立如图所示的空间直角坐标系
为单位长,建立如图所示的空间直角坐标系![]() .则
.则![]() .
.
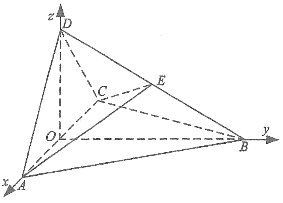
由题设知,四面体ABCE的体积为四面体ABCD的体积的![]() ,从而E到平面ABC的距离为D到平面ABC的距离的
,从而E到平面ABC的距离为D到平面ABC的距离的![]() ,即E为DB的中点,得
,即E为DB的中点,得![]() .
.
故![]() .
.
设![]() 是平面DAE的法向量,则
是平面DAE的法向量,则 即
即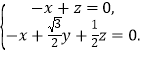
可取![]() .
.
设![]() 是平面AEC的法向量,则
是平面AEC的法向量,则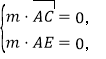 同理可取
同理可取![]() .
.
则![]() .
.
所以二面角D-AE-C的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如果函数![]() 在定义域内存在区间[a,b],使
在定义域内存在区间[a,b],使![]() 在[a,b]上的值域是[2a,2b],那么称
在[a,b]上的值域是[2a,2b],那么称![]() 为“倍增函数”。
为“倍增函数”。
(I)判断![]() =
=![]() 是否为“倍增函数”,并说明理由;
是否为“倍增函数”,并说明理由;
(II)证明:函数![]() =
=![]() 是“倍增函数”;
是“倍增函数”;
(III)若函数![]() =ln(
=ln(![]() )是“倍增函数”,写出实数m的取值范围。(只需写出结论)
)是“倍增函数”,写出实数m的取值范围。(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知斜率为1的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() ,椭圆
,椭圆![]() 的上顶点为
的上顶点为![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,若直线
两点,若直线![]() 与
与![]() 的斜率之和为2,证明:
的斜率之和为2,证明:![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C于A,B两点,圆M是以线段AB为直径的圆.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点P(4,-2),求直线l与圆M的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂产生的废气经过过滤后排放,规定排放时污染物的残留含量不得超过1%.已知在过滤过程中的污染物的残留数量P(单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为:![]() (
(![]() 为正常数,
为正常数,![]() 为原污染物数量).若前5个小时废气中的污染物被过滤掉了90%,那么要能够按规定排放废气,至少还需要过滤( )
为原污染物数量).若前5个小时废气中的污染物被过滤掉了90%,那么要能够按规定排放废气,至少还需要过滤( )
A. ![]() 小时B.
小时B. ![]() 小时C. 5小时D.
小时C. 5小时D. ![]() 小时
小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com