
【题目】设![]() 外接圆上三段弧
外接圆上三段弧![]() 的中点依次为
的中点依次为![]() ,其关于
,其关于![]() 的对称点依次为
的对称点依次为![]() .若顶点与对应旁切圆切点的连线交于一点
.若顶点与对应旁切圆切点的连线交于一点![]() (界心),
(界心),![]() 为
为![]() 的垂心,证明:
的垂心,证明:![]() 在以
在以![]() 为直径的圆上.
为直径的圆上.
【答案】见解析
【解析】
记![]() 的三边长为
的三边长为![]() ,
,![]() ,
,![]() 为
为![]() 的内心.
的内心.
先证明一个引理.
引理 顶点与界心连线平行且等于2倍内心与其对应边中点的连线.
证明:如图,设![]() 为
为![]() 的内心,
的内心,![]() 为
为![]() 的中点,
的中点,![]() 为切点,
为切点,![]() 为对应角平分线的交点,
为对应角平分线的交点,![]() 为旁切圆的切点,
为旁切圆的切点,![]() 为界心,
为界心,![]() 为
为![]() 与内切圆的交点.
与内切圆的交点.
对![]() 与截线
与截线![]() 应用梅涅劳斯定理得
应用梅涅劳斯定理得![]() .
.
将![]() ,
,![]() ,
,![]() ,代入上式化简得
,代入上式化简得![]()
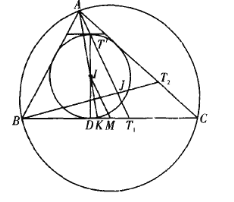
因为![]() 为
为![]() 的中点,
的中点,![]() 为切点,
为切点,![]() 为旁切圆的切点,所以,
为旁切圆的切点,所以,![]() .
.
由位似变换,知![]() 为
为![]() 的中点.
的中点.
故![]() .
.
回到原题.如图,延长![]() 与
与![]() 的延长线交于点
的延长线交于点![]() .
.
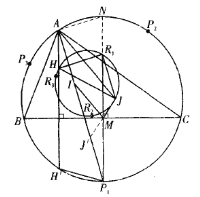
由引理,知![]() ,且
,且![]() 所以,
所以,![]() 为
为![]() 的中点.
的中点.
又点![]() 与
与![]() 关于
关于![]() 对称,于是.由对角线互柑平分的性质,知四边形
对称,于是.由对角线互柑平分的性质,知四边形![]() 为平行四边形.
为平行四边形.
因此, ![]() .
.
延长![]() 与外接圆交于点
与外接圆交于点![]() ,联结
,联结![]() .
.
因为![]() 为垂心,
为垂心,![]() 关于
关于![]() 的对称点
的对称点![]() 在外接圆上,所以,
在外接圆上,所以,![]() .
.
于是,![]() .则
.则![]() .
.
从而,四边形![]() 为平行四边形.
为平行四边形.
又![]() 为外接圆的直径,故
为外接圆的直径,故![]() .易知,
.易知, ![]() .
.
所以, ![]() ,
,
同理, ![]() ,
,![]() .故本题得证.
.故本题得证.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某中学将要举行校园歌手大赛,现有4男3女参加,需要安排他们的出场顺序.(结果用数字作答)
(1)如果3个女生都不相邻,那么有多少种不同的出场顺序?
(2)如果3位女生都相邻,且男生甲不在第一个出场,那么有多少种不同的出场顺序?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018以来,依托用户碎片化时间的娱乐需求、分享需求以及视频态的信息负载力,短视频快速崛起;与此同时,移动阅读方兴未艾,从侧面反应了人们对精神富足的一种追求,在习惯了大众娱乐所带来的短暂愉悦后,部分用户依旧对有着传统文学底蕴的严肃阅读青睐有加.某读书APP抽样调查了非一线城市![]() 和一线城市
和一线城市![]() 各100名用户的日使用时长(单位:分钟),绘制成频率分布直方图如下,其中日使用时长不低于60分钟的用户记为“活跃用户”.
各100名用户的日使用时长(单位:分钟),绘制成频率分布直方图如下,其中日使用时长不低于60分钟的用户记为“活跃用户”.
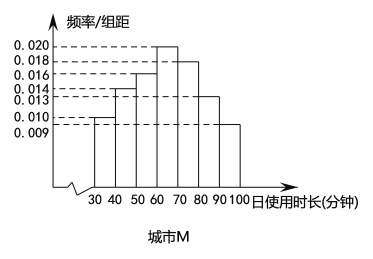
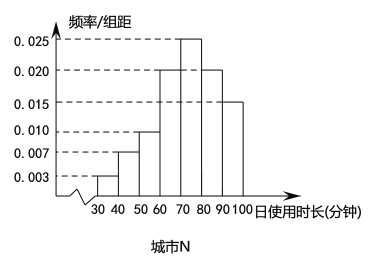
(1)请填写以下![]() 列联表,并判断是否有99%的把握认为用户活跃与否与所在城市有关?
列联表,并判断是否有99%的把握认为用户活跃与否与所在城市有关?
活跃用户 | 不活跃用户 | 合计 | |
城市 | |||
城市 | |||
合计 |
临界值表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
参考公式: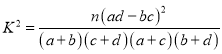 .
.
(2)以频率估计概率,从城市![]() 中任选2名用户,从城市
中任选2名用户,从城市![]() 中任选1名用户,设这3名用户中活跃用户的人数为
中任选1名用户,设这3名用户中活跃用户的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
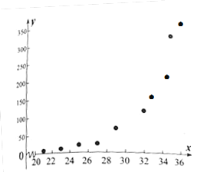
【题目】经观测,某昆虫的产卵数![]() 与温度
与温度![]() 有关,现将收集到的温度
有关,现将收集到的温度![]() 和产卵数
和产卵数![]() 的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
|
|
|
|
|
|
275 | 731.1 | 21.7 | 150 | 2368.36 | 30 |
表中![]() ,
,![]()
(1)根据散点图判断,![]() ,
,![]() 与
与![]() 哪一个适宜作为
哪一个适宜作为![]() 与
与![]() 之间的回归方程模型?(给出判断即可,不必说明理由)
之间的回归方程模型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据.
①试求![]() 关于
关于![]() 回归方程;
回归方程;
②已知用人工培养该昆虫的成本![]() 与温度
与温度![]() 和产卵数
和产卵数![]() 的关系为
的关系为![]() ,当温度
,当温度![]() (
(![]() 取整数)为何值时,培养成本的预报值最小?
取整数)为何值时,培养成本的预报值最小?
附:对于一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为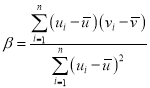 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,定点
,定点![]() ,定直线
,定直线![]() 和
和![]() 上的动点
上的动点![]() 满足:
满足:![]() 在直线
在直线![]() 的同侧,点
的同侧,点![]() 在直线
在直线![]() 的另一侧.以
的另一侧.以![]() 为焦点作与直线
为焦点作与直线![]() 相切的椭圆
相切的椭圆![]() ,且当
,且当![]() 在
在![]() 上运动时,椭圆
上运动时,椭圆![]() 的长轴长为定值.
的长轴长为定值.
(1)求直线![]() 的方程;
的方程;
(2)对于第一象限内任意2012个在椭圆![]() 上的点,是否一定可以将它们分成两组,使得其中一组点的横坐标之和不大于2013,另一组点的纵坐标之和不大于2013?请证明你的结论.
上的点,是否一定可以将它们分成两组,使得其中一组点的横坐标之和不大于2013,另一组点的纵坐标之和不大于2013?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若存在正数p,使得
,若存在正数p,使得![]() 对任意
对任意![]() 都成立,则称数列
都成立,则称数列![]() 为“拟等比数列”.
为“拟等比数列”.
![]() 已知
已知![]() ,
,![]() 且
且![]() ,若数列
,若数列![]() 和
和![]() 满足:
满足:![]() ,
,![]() 且
且![]() ,
,![]() .
.
![]() 若
若![]() ,求
,求![]() 的取值范围;
的取值范围;
![]() 求证:数列
求证:数列![]() 是“拟等比数列”;
是“拟等比数列”;
![]() 已知等差数列
已知等差数列![]() 的首项为
的首项为![]() ,公差为d,前n项和为
,公差为d,前n项和为![]() ,若
,若![]() ,
,![]() ,
,![]() ,且
,且![]() 是“拟等比数列”,求p的取值范围
是“拟等比数列”,求p的取值范围![]() 请用
请用![]() ,d表示
,d表示![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】11个兴趣班,若干学生参与(可重复参与),每个兴趣班人数相同(招满,人数未知).已知任意九个兴趣班包括了全体学生,而任意八个兴趣班没有包括全体学生求学生总人数的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com