练习册系列答案
相关习题
科目:高中数学
来源:2012-2013学年山东省高三第一次(3月)周测理科数学试卷(解析版)
题型:填空题
已知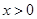 ,则
,则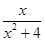 的最大值为_________________.
的最大值为_________________.
查看答案和解析>>
科目:高中数学
来源:2011-2012学年浙江省杭州市高三3月月考理科数学试卷
题型:填空题
已知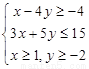 ,则
,则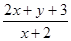 的最大值为 ▲ ;
的最大值为 ▲ ;
查看答案和解析>>
科目:高中数学
来源:2014届浙江省台州市高一上学期期末考试数学试卷
题型:选择题
已知 (
(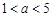 ),则
),则 的最大值为
的最大值为
A.2
B.3
C.4
D.6
查看答案和解析>>
科目:高中数学
来源:2013届山东省高二上学期期中文科数学试卷
题型:填空题
已知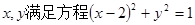 ,则
,则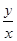 的最大值为
的最大值为
查看答案和解析>>
科目:高中数学
来源:2010年甘肃省天水市高二上学期第一阶段考试理科数学卷
题型:填空题
已知 ,则
,则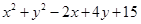 的最大值为___________.
的最大值为___________.
查看答案和解析>>

![]() ,则
,则![]() 的最大值为( )
的最大值为( ) ![]() B.
B.![]() C.
C.![]() D.
D.![]()