
| A. | 16π2 | B. | 4π2 | C. | 2π2 | D. | π2 |
分析 先利用定积分的几何意义计算定积分${∫}_{-2}^{2}$$\sqrt{4-{x}^{2}}$dx的值,然后利用等比数列的性质进行化简整理,可得结论.
解答 解:∵${∫}_{-2}^{2}$$\sqrt{4-{x}^{2}}$dx,表示以原点为圆心以2为半径的圆的面积的二分之一,
∴${∫}_{-2}^{2}$$\sqrt{4-{x}^{2}}$dx=$\frac{1}{2}$π×4=2π,
∴a5+a7=2π,
∵等比数列{an},
∴a6(a4+2a6+a8)=a6a4+2a62+a6a8=a52+2a5a7+a72=(a5+a7)2=4π2.
故选:B.
点评 本小题主要考查定积分、定积分的几何意义、圆的面积等基础知识,以及等比数列的性质,同时考查了运算求解的能力,属于基础题.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y=0 | B. | x+2y=0 | C. | 2x+y=0 | D. | 2x-y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
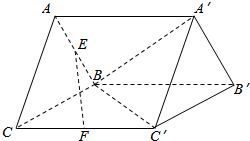 如图,三棱柱ABC-A′B′C′,BC=1,BC′=1,CC′=$\sqrt{2}$,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.
如图,三棱柱ABC-A′B′C′,BC=1,BC′=1,CC′=$\sqrt{2}$,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 0 | C. | 4 | D. | -20102 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了调查一款项链的销售数量x(件)与销售利润y(万元)之间的相关关系,某公司的市场专员作出调查并将结果统计如表所示:
为了调查一款项链的销售数量x(件)与销售利润y(万元)之间的相关关系,某公司的市场专员作出调查并将结果统计如表所示:| x(件) | 3 | 4 | 5 | 6 | 8 | 10 |
| y(万元) | 3 | 2 | 4 | 6 | 7 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com