解:(1)∵a
1=λ,∴
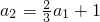
=
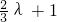
,
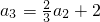
=
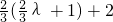
=
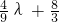
.
∵数列{a
n}前三项成等差数列,∴2a
2=a
1+a
3,
∴
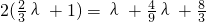
,解得λ=-6.
∴λ的值为-6.
(2)由(1)可知:若λ=-6,则a
n=-6+3(n-1)=3n-9,此时b
n=0不是等比数列;
当λ≠-6时,a
n≠3n-9.
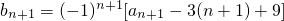
=
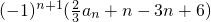
=
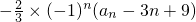
=-
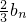
.
又b
1=-(a
1-3+9)=-λ-6≠0,
∴数列{b
n}是以-λ-6为首项,

为公比的等比数列.
(3)由(1)(2)可知:①当λ=-6时,b
n=0,对于给定的0<a<b,对任意正整数n,0<a<S
n<b不成立.
②当λ≠-6时,假设存在实数λ,使得对任意正整数n,都有a<S
n<b成立.
由(2)可知:数列{b
n}是以-λ-6为首项,

为公比的等比数列,∴
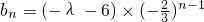
=
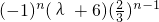
.
∴S
n=(-λ-6)
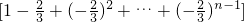
=
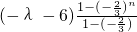
=
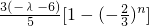
.
当n→+∞时,
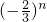
→0.
当λ>-6时,S
n<0,此时对任意正整数n,a<S
n<b不成立.
当λ<-6时,n=2k(k∈N
*)时,∵

,∴0<

;
n=2k-1(k∈N
*)时,
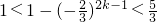
,∴
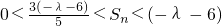
.
∵

<(-λ-6).
∴对于任意正整数n,
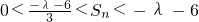
.
∵设0<a<b,S
n为数列{b
n}的前n项和,使得对任意正整数n,都有a<S
n<b.
∴必有
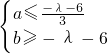
,解得-6-b≤λ≤-3a-6.
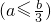
.
分析:(1)利用等差数列的定义及其通项公式即可得出;
(2)由(1)可知:若λ=-6,数列{b
n}不是等比数列;当λ≠-6时,利用递推关系可找出b
n+1与b
n的关系即可;
(3)对λ分λ=-6与λ≠-6讨论,利用等比数列的前n项和公式即可得出.
点评:数列掌握等差数列的定义及其通项公式、等比数列与等差数列的前n项和公式、分类讨论的思想方法、递推关系是解题的关键.

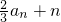 ,bn=(-1)n(an-3n+9),其中λ为实数,n为正整数.
,bn=(-1)n(an-3n+9),其中λ为实数,n为正整数.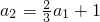 =
=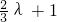 ,
,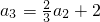 =
=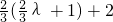 =
=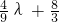 .
.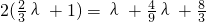 ,解得λ=-6.
,解得λ=-6.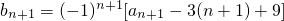 =
=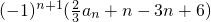 =
=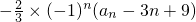 =-
=-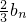 .
. 为公比的等比数列.
为公比的等比数列. 为公比的等比数列,∴
为公比的等比数列,∴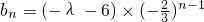 =
=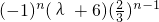 .
.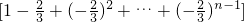 =
=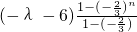 =
=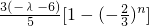 .
.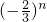 →0.
→0. ,∴0<
,∴0< ;
;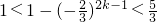 ,∴
,∴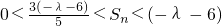 .
. <(-λ-6).
<(-λ-6).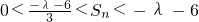 .
.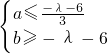 ,解得-6-b≤λ≤-3a-6.
,解得-6-b≤λ≤-3a-6.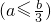 .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案