
【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当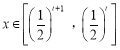 时,求函数
时,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在非负实数![]() 、
、![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,若存在,求出
,若存在,求出![]() 、
、![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
【答案】⑴![]() ;⑵
;⑵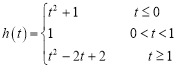 ;⑶存在
;⑶存在![]() 满足题意.
满足题意.
【解析】
试题分析:对问题⑴,根据题目条件首先要对实数![]() 的取值进行分类讨论,再结合极端不等式恒成立即可求出函数
的取值进行分类讨论,再结合极端不等式恒成立即可求出函数![]() 的定义域为
的定义域为![]() 时实数
时实数![]() 的取值范围;对于问题⑵,根据二次函数的单调性并结合对参数
的取值范围;对于问题⑵,根据二次函数的单调性并结合对参数![]() 的分类讨论,即可求得函数
的分类讨论,即可求得函数![]() 的最小值
的最小值![]() ;对问题⑶,根据二次函数的单调性以及函数与方程的思想即可知道存在符合题意的实数
;对问题⑶,根据二次函数的单调性以及函数与方程的思想即可知道存在符合题意的实数![]() 、
、![]() 的值.
的值.
试题解析:⑴![]() 定义域为
定义域为![]() .
.
所以![]() 对一切
对一切![]() 成立. ……………………1分
成立. ……………………1分
当![]() 时,
时,![]() 不可能对一切
不可能对一切![]() 成立. ……………………2分
成立. ……………………2分
所以![]() ,即
,即![]() 解得
解得![]() .
.
综上![]() . ……………………4分
. ……………………4分
⑵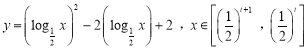 ,
,
令![]() ,
,
所以![]() ……………………5分
……………………5分
当![]() 时,
时,![]() . ……………………6分
. ……………………6分
当![]() 时,
时,![]() . ……………………7分
. ……………………7分
当![]() 时,
时,![]() . ……………………8分
. ……………………8分
所以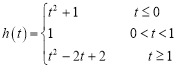 ……………………9分
……………………9分
⑶![]() 在
在![]() 上是增函数,
上是增函数,
若存在非负实数![]() 、
、![]() 满足题意,则
满足题意,则![]() ,………………………………10分
,………………………………10分
即![]() 、
、![]() 是方程
是方程![]() 的两非负实根,且
的两非负实根,且![]() ,
,
所以![]() .
.
即存在![]() 满足题意………………………………12分.
满足题意………………………………12分.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(1)若方程![]() 有三个解,试求实数
有三个解,试求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,
,![]() (
(![]() ),使函数
),使函数![]() 的定义域与值域均为
的定义域与值域均为![]() ?若存在,求出所有的区间
?若存在,求出所有的区间![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的右焦点为
的右焦点为![]() ,离心率
,离心率![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的弦长为1.
截得的弦长为1.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)记椭圆![]() 的上,下顶点分别为A,B,设过点
的上,下顶点分别为A,B,设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 分别交于点
分别交于点![]() ,求证:直线
,求证:直线![]() 必定过一定点,并求该定点的坐标.
必定过一定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面是一段演绎推理:
大前提:如果直线平行于平面,则这条直线平行于平面内的所有直线;
小前提:已知直线b∥平面α,直线a平面α;
结论:所以直线b∥直线a.在这个推理中( )
A. 大前提正确,结论错误 B. 大前提错误,结论错误
C. 大、小前提正确,只有结论错误 D. 小前提与结论都是错误的
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个地区共有5个乡镇,共30万人,其人口比例为3∶2∶5∶2∶3,从这30万人中抽取一个300人的样本,分析某种疾病的发病率.已知这种疾病与不同的地理位置及水土有关,则应采取什么样的抽样方法?并写出具体过程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 中,棱长
中,棱长![]() ,过点
,过点![]() 的平面
的平面![]() 与正方体的面相交,交线围成一个正三角形.
与正方体的面相交,交线围成一个正三角形.

(1)在图中画出这个正三角形(不必说明画法和理由);
(2)平面![]() 将该正方体截成两个几何体,求体积较大的几何体的体积和表面积.
将该正方体截成两个几何体,求体积较大的几何体的体积和表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列表述正确的是( )
①归纳推理是由部分到整体的推理; ②归纳推理是由一般到一般的推理;
③演绎推理是由一般到特殊的推理; ④类比推理是由特殊到一般的推理;
⑤类比推理是由特殊到特殊的推理.
A. ①②③ B. ②③④ C. ②④⑤ D. ①③⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把平面几何里相似的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就称它们是相似体,给出下面的几何体:
①两个球体;②两个长方体;③两个正四面体;④两个正三棱柱;⑤两个正四棱锥,则一定是相似体的个数是( )
A. 4 B. 2 C. 3 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】读下面的程序:
i=1
S=0
DO
INPUT x
S=S+x
i=i+1
LOOP UNTIL i>10
A=S/10
PRINT A
END
该程序的作用是
A. 计算9个数的和 B. 计算9个数的平均数
C. 计算10个数的和 D. 计算10个数的平均数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com