
 ,AA1=4,点D是AB的中点
,AA1=4,点D是AB的中点 的平面角的正切值
的平面角的正切值


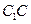 ,且
,且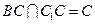
 平面BCC1 ……………………………………4分
平面BCC1 ……………………………………4分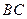 中点
中点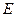 ,过
,过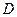 作
作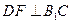 于
于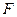 ,连接
,连接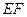
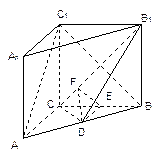

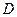 是
是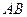 中点,
中点,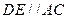 ,又
,又 平面
平面
 平面
平面 ,
, 
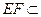 平面
平面 ,
, 平面
平面
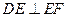
 又
又
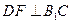 且
且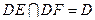
 平面
平面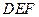 ,
,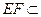 平面
平面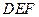
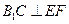 又
又
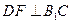
 是二面角
是二面角 的平面角 …………………………10分
的平面角 …………………………10分 AC=3,BC=4,AA1=4,
AC=3,BC=4,AA1=4,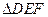 中,
中,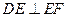 ,
,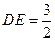 ,
,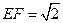
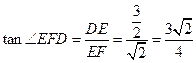 ……………………………………11分
……………………………………11分 的正切值
的正切值 ………………………………12分
………………………………12分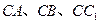 分别为
分别为 轴建立如图所示空间直角坐标系 ………6分
轴建立如图所示空间直角坐标系 ………6分 AC=3,BC=4,AA1=4,
AC=3,BC=4,AA1=4,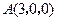 ,
,

 ,
, ,
,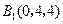 ,
,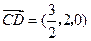 ,
,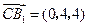 平面
平面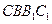 的法向量
的法向量  , …………………7分
, …………………7分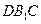 的法向量
的法向量 ,
, ,
, 的夹角(或其补角)的大小就是二面角
的夹角(或其补角)的大小就是二面角 的大小 ……8分
的大小 ……8分 令
令 ,则
,则 ,
,
 …………10分
…………10分 ,则
,则 ……………
…………… 11分
11分
 是锐二面角
是锐二面角 的正切值为
的正切值为 …………………… 12分
…………………… 12分 

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源:不详 题型:解答题
 是圆柱的母线,
是圆柱的母线, 是圆柱底面圆的直径,
是圆柱底面圆的直径, 是底面圆周上异于
是底面圆周上异于 的任意一点,
的任意一点,
 平面
平面 ;
; 的体积的最大值.
的体积的最大值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题





 ;
; 上是否存在点
上是否存在点 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. 

 使
使 若存在,求出
若存在,求出 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
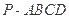 中,
中,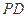 ⊥底面
⊥底面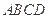
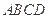 为正方形,
为正方形,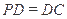 ,
,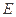 ,
,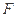 分别是
分别是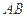
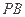 的中点.
的中点.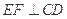 ;(2)设PD="AD=a," 求三棱锥B-EFC的体积.
;(2)设PD="AD=a," 求三棱锥B-EFC的体积.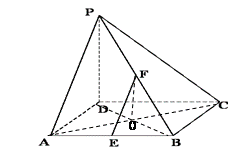
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com