
 ,则抛物线C的方程为________,若点P在抛物线C上运动,点Q在直线x+y+5=0上运动,则|PQ|的最小值等于________.
,则抛物线C的方程为________,若点P在抛物线C上运动,点Q在直线x+y+5=0上运动,则|PQ|的最小值等于________.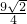
 ,得
,得 ,从而求得p值,设与直线x+y+5=0平行的抛物线的切线方程为x+y+m=0,直线x+y+5=0与切线距离即为|PQ|的最小值,联立切线方程与抛物线方程消掉x得y的二次方程,令△=0可求得m值,从而得切线方程,根据两点间距离公式即可求得答案.
,从而求得p值,设与直线x+y+5=0平行的抛物线的切线方程为x+y+m=0,直线x+y+5=0与切线距离即为|PQ|的最小值,联立切线方程与抛物线方程消掉x得y的二次方程,令△=0可求得m值,从而得切线方程,根据两点间距离公式即可求得答案. ,
, ,解得p=1,
,解得p=1,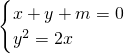 得y2+2y+2m=0,
得y2+2y+2m=0, ,
, =0,
=0,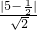 =
=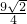 ,即为|PQ|的最小值.
,即为|PQ|的最小值.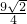 .
.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:
| 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ) | 2 |
| ) | 2 |
| r | 2 |
| y | 2 |
查看答案和解析>>
科目:高中数学 来源:上海市进才中学2007届高三理科月考六数学试题 题型:044
已知抛物线C:y2=2px(p>0),直线l交C于E、F两点.
(1)求证:命题“若直线l过点A(2p,0),则∠EOF=90°(O为坐标原点)”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由;
(3)将点A(2p,0)向右或向左移动为点A(c,0),直线l过点A交C于E、F两点.当c>2p及0<c<2p时,分别猜测∠EOF大小的变化情况(只须写出结论,不必证明).
查看答案和解析>>
科目:高中数学 来源:2011年高三数学复习(第8章 圆锥曲线):8.7 求轨迹方程(一)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com