
设 ,其中
,其中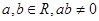 . 若
. 若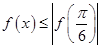 对一切
对一切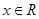 恒成立,则 ①
恒成立,则 ① 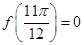 ;
②
;
② 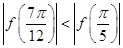 ;
③
;
③ 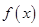 既不是奇函数也不是偶函数;④
既不是奇函数也不是偶函数;④ 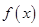 的单调递增区间是
的单调递增区间是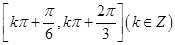 ;⑤ 存在经过点
;⑤ 存在经过点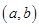 的直线与函数
的直线与函数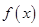 的图象不相交.
的图象不相交.
以上结论正确的是__________________(写出所有正确结论的编号).
科目:高中数学 来源: 题型:
| 4 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| i |
| n+1-i |
| 1 |
| 2 |
| 3 |
| n+1-3 |
| 11λ-3n2 |
| (n+1)(n+2) |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省鹤岗一中高一(上)期末数学试卷(文科)(解析版) 题型:填空题
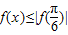 对一切x∈R恒成立,则
对一切x∈R恒成立,则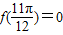 ;
;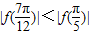 ;
;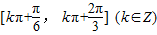 ;
;查看答案和解析>>
科目:高中数学 来源:2008年北京市朝阳区高考数学二模试卷(文科)(解析版) 题型:解答题
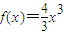 +ax-1(a∈R),其中f'(x)是f(x)的导函数.
+ax-1(a∈R),其中f'(x)是f(x)的导函数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com