
【题目】如图,抛物线![]() 的焦点为F,准线为
的焦点为F,准线为![]() ,
,![]() 交x轴于点A,并截圆
交x轴于点A,并截圆![]() 所得弦长为
所得弦长为![]() ,M为平面内动点,△MAF周长为6.
,M为平面内动点,△MAF周长为6.
(1)求抛物线![]() 方程以及点M的轨迹
方程以及点M的轨迹![]() 的方程;
的方程;
(2)“过轨迹![]() 的一个焦点
的一个焦点![]() 作与
作与![]() 轴不垂直的任意直线
轴不垂直的任意直线![]() ”交轨迹
”交轨迹![]() 于
于![]() 两点,线段
两点,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,则
,则![]() 为定值,且定值是
为定值,且定值是![]() ”.命题中涉及了这么几个要素:给定的圆锥曲线
”.命题中涉及了这么几个要素:给定的圆锥曲线![]() ,过该圆锥曲线焦点
,过该圆锥曲线焦点![]() 的弦
的弦![]() ,
,![]() 的垂直平分线与焦点所在的对称轴的焦点
的垂直平分线与焦点所在的对称轴的焦点![]() ,
,![]() 的长度与
的长度与![]() 、
、![]() 两点间距离的比值.试类比上述命题,写出一个关于抛物线
两点间距离的比值.试类比上述命题,写出一个关于抛物线![]() 的类似的正确命题,并加以证明.
的类似的正确命题,并加以证明.
(3)试推广(2)中的命题,写出关于抛物线的一般性命题(不必证明).
【答案】(1)![]() ,
,![]() ;(2)过抛物线
;(2)过抛物线![]() 的焦点
的焦点![]() 作与
作与![]() 轴不垂直的任意直线
轴不垂直的任意直线![]() ,交抛物线于
,交抛物线于![]() 两点,线段
两点,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,则
,则![]() 为定值,且定值为
为定值,且定值为![]() ,证明见解析;(3)过抛物线的焦点
,证明见解析;(3)过抛物线的焦点![]() 作与对称轴不垂直的任意直线
作与对称轴不垂直的任意直线![]() ,交抛物线于
,交抛物线于![]() 两点,线段
两点,线段![]() 的垂直平分线交对称轴于点
的垂直平分线交对称轴于点![]() ,则
,则![]() 为定值,且定值为
为定值,且定值为![]() .
.
【解析】
(1)根据弦长公式可求出弦心距,即得准线![]() 的方程和点
的方程和点![]() 的坐标,从而可求出抛物线方程,再根据△MAF周长为6,设出点
的坐标,从而可求出抛物线方程,再根据△MAF周长为6,设出点![]() ,根据椭圆的定义即可求出点M的轨迹
,根据椭圆的定义即可求出点M的轨迹![]() 的方程;
的方程;
(2)根据题意类比即可写出;
(3)利用(2)中原理,即可写出.
(1)设圆心到直线![]() 的距离为
的距离为![]() ,∴
,∴![]() ,解得
,解得![]() .
.
所以准线![]() :
:![]() ,点
,点![]() ,点
,点![]() ,即有
,即有![]() ,∴
,∴![]() ,即抛物线
,即抛物线![]() .
.
因为![]() ,所以
,所以![]() ,即点
,即点![]() 的轨迹是以点
的轨迹是以点![]() 为焦点,长轴长为
为焦点,长轴长为![]() ,焦距为
,焦距为![]() 的椭圆,∴
的椭圆,∴![]() ,解得
,解得![]() ,即有
,即有![]() .
.
故点M的轨迹![]() 的方程为
的方程为![]() .
.
(2)关于抛物线![]() 的类似的正确命题为:过抛物线
的类似的正确命题为:过抛物线![]() 的焦点
的焦点![]() 作与
作与![]() 轴不垂直的任意直线
轴不垂直的任意直线![]() ,交抛物线于
,交抛物线于![]() 两点,线段
两点,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,则
,则![]() 为定值,且定值为
为定值,且定值为![]() .证明如下:
.证明如下:
如图所示:
设直线![]() :
:![]()
由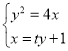 得,
得,![]() ,设
,设![]() ,
,
所以![]() ,
,![]() ,
,
即![]() 的中点坐标为
的中点坐标为![]() ,
,
![]() 的垂直平分线的方程为:
的垂直平分线的方程为:![]() ,令
,令![]() ,解得
,解得![]() ,
,
∴![]() .
.
又因为![]() ,所以
,所以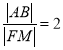 .
.
(3)过抛物线的焦点![]() 作与对称轴不垂直的任意直线
作与对称轴不垂直的任意直线![]() ,交抛物线于
,交抛物线于![]() 两点,线段
两点,线段![]() 的垂直平分线交对称轴于点
的垂直平分线交对称轴于点![]() ,则
,则![]() 为定值,且定值为
为定值,且定值为![]() .
.


科目:高中数学 来源: 题型:
【题目】《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”;四个面均为直角三角形的四面体称为“鳖膈”.如图在堑堵ABC-A1B1C1中,AC⊥BC,且AA1=AB=2.下列说法正确的是( )
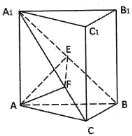
A.四棱锥B-A1ACC1为“阳马”
B.四面体A1C1CB为“鳖膈”
C.四棱锥B-A1ACC1体积最大为![]()
D.过A点分别作AE⊥A1B于点E,AF⊥A1C于点F,则EF⊥A1B
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,动圆
,动圆![]() 与圆
与圆![]() 内切且与圆
内切且与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() 与
与![]() 为平面内的两个定点,过
为平面内的两个定点,过![]() 点的直线
点的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,抛物线C:
,抛物线C:![]() 的焦点到直线l:
的焦点到直线l:![]() 的距离为
的距离为![]() .
.
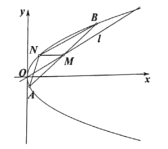
(1)求m的值.
(2)如图,已知抛物线C的动弦![]() 的中点M在直线l上,过点M且平行于x轴的直线与抛物线C相交于点N,求
的中点M在直线l上,过点M且平行于x轴的直线与抛物线C相交于点N,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且其离心率为
,且其离心率为![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别相交于
分别相交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在圆心在原点的定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】健身馆某项目收费标准为每次60元,现推出会员优惠活动:具体收费标准如下:
消费次数 | 第1次 | 第2次 | 第3次 | 不少于4次 |
收费比例 | 0.95 | 0.90 | 0.85 | 0.80 |
现随机抽取了100位会员统计它们的消费次数,得到数据如下:
消费次数 | 1次 | 2次 | 3次 | 不少于4次 |
频数 | 60 | 25 | 10 | 5 |
假设该项目的成本为每次30元,根据给出的数据回答下列问题:
(1)估计1位会员至少消费两次的概率
(2)某会员消费4次,求这4次消费获得的平均利润;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离的比值为
的距离的比值为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 交于两点
交于两点![]() ,
,![]() ,设点
,设点![]() ,
,![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,
,![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为广泛开展垃圾分类的宣传教育和倡导工作,使市民树立垃圾分类的环保意识,学会垃圾分类的知识,特举办了“垃圾分类知识竞赛".据统计,在为期1个月的活动中,共有两万人次参与网络答题.市文明实践中心随机抽取100名参与该活动的市民,以他们单次答题得分作为样本进行分析,由此得到如图所示的频率分布直方图:

(1)求图中a的值及参与该活动的市民单次挑战得分的平均成绩![]() (同一组中数据用该组区间中点值作代表);
(同一组中数据用该组区间中点值作代表);
(2)若垃圾分类答题挑战赛得分落在区间![]() 之外,则可获得一等奖奖励,其中
之外,则可获得一等奖奖励,其中![]() ,s分别为样本平均数和样本标准差,计算可得
,s分别为样本平均数和样本标准差,计算可得![]() ,若某人的答题得分为96分,试判断此人是否获得一等奖;
,若某人的答题得分为96分,试判断此人是否获得一等奖;
(3)为扩大本次“垃圾分类知识竞赛”活动的影响力,市文明实践中心再次组织市民组队参场有奖知识竞赛,竞赛共分五轮进行,已知“光速队”与“超能队”五轮的成绩如下表:
成绩 | 第一轮 | 第二轮 | 第三轮 | 第四轮 | 第五轮 |
“光速队” | 93 | 98 | 94 | 95 | 90 |
“超能队” | 93 | 96 | 97 | 94 | 90 |
①分别求“光速队”与“超能队”五轮成绩的平均数和方差;
②以上述数据为依据,你认为"光速队”与“超能队”的现场有奖知识竞赛成绩谁更稳定?
查看答案和解析>>
科目:高中数学 来源: 题型:
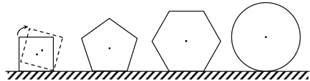
【题目】现有边长均为1的正方形正五边形正六边形及半径为1的圆各一个,在水平桌面上无滑动滚动一周,它们的中心的运动轨迹长分别为![]() ,
,![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com