练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】有下列命题：

    ①函数与的图象关于轴对称；

    ②若函数，则，都有；

    ③若函数，在上单调递增，则；

    ④若函数，则函数的最小值为．

    其中真命题的序号是______．

    【答案】②④

    【解析】

    根据函数与的图象关于轴对称和图象的平移变换可判断出①的正误，利用基本不等式可得②的正误，由函数在区间上单调递增，可得，然后可判断出③的正误，将函数图象左右平移，函数的最大值最小值不变，故函数与函数的最小值相同，即可得出④的正误.

    函数与的图象关于轴对称，将函数与的图象都向右平移2个单位，

    便得函数与的图象，所以函数与的图象关于对称，故①错误；

    若函数，则，都有，故②正确

    函数在区间上单调递增，所以，从而，故③错误

    将函数图象左右平移，函数的最大值最小值不变，

    所以函数与函数的最小值相同，为，故④正确

    故答案为：②④

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四棱锥中， 平面是的中点， 是上的点且为边上的高.

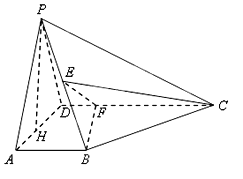
    （1）证明： 平面；

    （2）若，求三棱锥的体积；

    （3）在线段上是否存在这样一点，使得平面?若存在，说出点的位置.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求的极值；

    （2）若，求正实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数和有相同的公切线，则实数a的取值范围为_____________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）

    设函数f（x）=x+ax2+blnx，曲线y=f（x）过P（1,0），且在P点处的切斜线率为2.

    （I）求a，b的值；

    （II）证明：f(x)≤2x-2。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在底面为菱形的四棱锥P-ABCD中，平面平面ABCD，为等腰直角三角形，，，点E，F分别为BC，PD的中点，直线PC与平面AEF交于点Q.

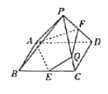
    （1）若平面平面，求证：.

    （2）求直线AQ与平面PCD所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论的单调性；

    （2）若，设，证明：，，使.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某超市在节日期间进行有奖促销，凡在该超市购物满400元的顾客，将获得一次摸奖机会，规则如下：奖盒中放有除颜色外完全相同的1个红球，1个黄球，1个白球和1个黑球顾客不放回的每次摸出1个球，若摸到黑球则停止摸奖，否则就继续摸球规定摸到红球奖励20元，摸到白球或黄球奖励10元，摸到黑球不奖励

    （1）求1名顾客摸球2次停止摸奖的概率：

    （2）记为1名顾客5次摸奖获得的奖金数额，求随机变量的分布列和数学期望

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC的角A、B、C的对边分别为a、b、c，＝(2b－c，a)，＝(cosA，－cosC)，且⊥．

    (Ⅰ)求角A的大小；

    (Ⅱ)当y＝2sin2B＋sin(2B＋)取最大值时，求角的大小.

    查看答案和解析>>

    同步练习册答案