
【题目】已知a>0,且a≠1,函数 ![]() ,设函数f(x)的最大值为M,最小值为N,则( )
,设函数f(x)的最大值为M,最小值为N,则( )
A.M+N=8
B.M+N=10
C.M﹣N=8
D.M﹣N=10
【答案】A
【解析】解: ![]() ,
,
令g(x)=ln( ![]() ﹣2x),x∈[﹣1,1],
﹣2x),x∈[﹣1,1],
由g(﹣x)=ln( ![]() +2x)=ln
+2x)=ln ![]()
=﹣ln( ![]() ﹣2x)=﹣g(x),
﹣2x)=﹣g(x),
可知g(﹣x)=﹣g(x),
故g(x)函数的图象关于原点对称,
设g(x)的最大值是a,则g(x)的最小值是﹣a,
由 ![]() =5﹣
=5﹣ ![]() ,
,
令h(x)=﹣ ![]() ,
,
0<a<1时,h(x)在[﹣1,1]递减,
h(x)的最小值是h(﹣1)=﹣ ![]() ,
,
h(x)的最大值是h(1)=﹣ ![]() ,
,
故h(﹣1)+h(1)=﹣2,
∴f(x)的最大值与最小值的和是10﹣2=8,
a>1时,h(x)在[﹣1,1]递增,
h(x)的最大值是h(﹣1)=﹣ ![]() ,
,
h(x)的最小值是h(1)=﹣ ![]() ,
,
故h(﹣1)+h(1)=﹣2,
故函数f(x)的最大值与最小值之和为8,
综上:函数f(x)的最大值与最小值之和为8,
故选:A.
【考点精析】利用函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣ax+cosx(a∈R),x∈[﹣
﹣ax+cosx(a∈R),x∈[﹣ ![]() ,
, ![]() ].
].
(1)若函数f(x)是偶函数,试求a的值;
(2)当a>0时,求证:函数f(x)在(0, ![]() )上单调递减.
)上单调递减.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣x+ ![]() +1(a∈R).
+1(a∈R).
(1)讨论f(x)的单调性与极值点的个数;
(2)当a=0时,关于x的方程f(x)=m(m∈R)有2个不同的实数根x1 , x2 , 证明:x1+x2>2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在高二年级实行选课走班教学,学校为学生提供了多种课程,其中数学科提供5种不同层次的课程,分别称为数学1、数学2、数学3、数学4、数学5,每个学生只能从这5种数学课程中选择一种学习,该校高二年级1800名学生的数学选课人数统计如表:
课程 | 数学1 | 数学2 | 数学3 | 数学4 | 数学5 | 合计 |
选课人数 | 180 | 540 | 540 | 360 | 180 | 1800 |
为了了解数学成绩与学生选课情况之间的关系,用分层抽样的方法从这1800名学生中抽取了10人进行分析.
(1)从选出的10名学生中随机抽取3人,求这3人中至少有2人选择数学2的概率;
(2)从选出的10名学生中随机抽取3人,记这3人中选择数学2的人数为X,选择数学1的人数为Y,设随机变量ξ=X﹣Y,求随机变量ξ的分布列和数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的中位数是83,乙班学生成绩的平均数是86,则x+y的值为( ) 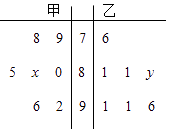
A.168
B.169
C.8
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x>0).
(x>0).
(1)试判断函数f(x)在(0,+∞)上单调性并证明你的结论;
(2)若f(x)> ![]() 恒成立,求整数k的最大值;
恒成立,求整数k的最大值;
(3)求证:(1+1×2)(1+2×3)…[1+n(n+1)]>e2n﹣3 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将分别标有“孔”“孟”“之”“乡”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀,随机摸出一球,不放回;再随机摸出一球,两次摸出的球上的汉字组成“孔孟”的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数fn(x)=﹣xn+3ax(a∈R,n∈N+),若对任意的x1 , x2∈[﹣1,1],都有|f3(x1)﹣f3(x2)|≤1,则a的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com