
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:高中数学 来源: 题型:013
甲、乙两名篮球队员轮流投篮,至某人投中为止,每次投篮甲投中的概率为0.4,乙投中的概率为0.6,而且不受其他投篮结果的影响,设甲投篮的次数为ξ,若甲先投,则P(ξ=k)等于( )
A.0.6k-1´0.4 B.0.24k-1´0.76 C.0.4k-1´0.6 D.0.76k-1´0.24
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
A.0.6k-1´0.4 B.0.24k-1´0.76 C.0.4k-1´0.6 D.0.76k-1´0.24
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学选修2-3 2.2二项分布及其应用练习卷(解析版) 题型:选择题
甲、乙两名篮球队员轮流投篮直至某人投中为止,设甲每次投篮命中的概率为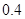 ,乙投中的概率为
,乙投中的概率为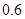 ,而且不受其他次投篮结果的影响,设投篮的轮数为
,而且不受其他次投篮结果的影响,设投篮的轮数为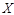 ,若甲先投,则
,若甲先投,则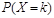 等于( )
等于( )
A.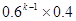 B. 0.24k-1×0.4
C.
B. 0.24k-1×0.4
C. 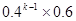 D.
D. 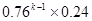
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com