练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知一条直线经过两条直线l1：2x-3y-4=0和l2：x+3y-11=0的交点，并且垂直于这个交点和原点的连线，求此直线方程．
    【答案】分析：由题意先求交点的坐标，再由垂直于这个交点和原点的连线求出直线的斜率，求出直线的方程．
    解答：解：设所求直线的斜率为k，交点为P（x，y），
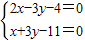
    由方程组，解得P（5，2）．
    故．
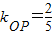
    因直线与直线OP垂直，则，
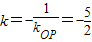
    所以所求直线的方程为，
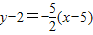
    即5x+2y-29=0，
    答：此直线的方程为5x+2y-29=0．
    点评：本题考查了直线垂直的条件，求直线的交点坐标和直线的点斜式方程，结果要化为一般式方程．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知一条直线经过两条直线l1：2x-3y-4=0和l2：x+3y-11=0的交点，并且垂直于这个交点和原点的连线，求此直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知一条直线经过两条直线l1：2x-3y-4=0和l2：x+3y-11=0的交点，并且垂直于这个交点和原点的连线，求此直线方程．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知一条直线经过两条直线l1：2x-3y-4=0和l2：x+3y-11=0的交点，并且垂直于这个交点和原点的连线，求此直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分14分）

    已知一条直线经过两条直线和的交点，并且垂直于这个交点和原点的连线，求此直线方程。

    查看答案和解析>>

    同步练习册答案