
【题目】如图所示的多面体ABCDEF满足:正方形ABCD与正三角形FBC所在的两个平面互相垂直,FB∥AE且FB=2EA.
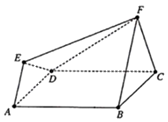
(1)证明:平面EFD⊥平面ABFE;
(2)求二面角E﹣FD﹣C的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)先证明AB⊥平面BCF,然后可得平面EFD⊥平面ABFE;
(2)建立空间直角坐标系,求解平面的法向量,然后利用向量的夹角公式可求.
(1)由题可得,因为ABCD是正方形且三角形FBC是正三角形,所以BC∥AD,BC=AD,FB=BC且∠FBC=60°,
又因为EA∥FB,2EA=FB,所以∠EAD=60°,在三角形EAD中,根据余弦定理可得:ED⊥AE.
因为平面ABCD⊥平面FBC,AB⊥BC,平面ABCD∩平面FBC=BC,且AB平面ABCD,所以AB⊥平面BCF,
因为BC∥AD, E A∥FB,FB∩BC=B,且FB、BC平面FCB,EA、AD平面EAD,所以平面EAD∥平面FBC,所以AB⊥平面EAD,
又因为ED平面EAD,所以AB⊥ED,
综上:ED⊥AE,ED⊥AB,EA∩AB=A且EA、AB平面ABFE,所以DE⊥平面ABFE,
又DE平面DEF,所以平面EFD⊥平面ABFE.
(2)如图,分别取BC和AD的中点O,G,连接OF,OG,
因为BO=OC且三角形FBC为正三角形,所以FO⊥BC,
因为AG=GD,BO=OC,所以OG∥AB,
由(1)可得,AB⊥平面FBC,则OG⊥平面FBC,
故OF、OB、OG两两垂直,分别以OB、OG、OF所在直线为x,y,z轴建立如图所示的空间直角坐标系,

不妨设BC=4,则![]() ,
,![]()
设平面DEF的法向量为![]() ,平面DCF的法向量为
,平面DCF的法向量为![]() ,
,
则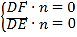
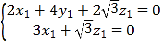
![]() ,
,
则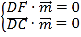
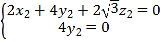
![]() ,
,
所以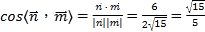
又二面角E﹣FD﹣C是钝二面角,所以二面角E﹣FD﹣C的余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与上下顶点构成直角三角形,以椭圆E的长轴为直径的圆与直线
的一个焦点与上下顶点构成直角三角形,以椭圆E的长轴为直径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)![]() 为椭圆
为椭圆![]() 上不同的三点,
上不同的三点,![]() 为坐标原点,若
为坐标原点,若![]() ,试问:
,试问:![]() 的面积是否为定值?若是,请求出定值;若不是,请说明理由.
的面积是否为定值?若是,请求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次高三年级统一考试中,数学试卷有一道满分10分的选做题,学生可以从![]() ,
,![]() 两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名考生的选做题成绩中随机抽取一个容量为10的样本,为此将900名考生选做题的成绩按照随机顺序依次编号为001—900.
两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名考生的选做题成绩中随机抽取一个容量为10的样本,为此将900名考生选做题的成绩按照随机顺序依次编号为001—900.
(1)若采用随机数表法抽样,并按照以下随机数表,以加粗的数字5为起点,从左向右依次读取数据,每次读取三位随机数,一行读数用完之后接下一行左端.写出样本编号的中位数;
05 26 93 70 60 22 35 85 15 13 92 03 51 59 77 59 56 78 06 83 52 91 05 70 74
07 97 10 88 23 09 98 42 99 64 61 71 62 99 15 06 51 29 16 93 58 05 77 09 51
51 26 87 85 85 54 87 66 47 54 73 32 08 11 12 44 95 92 63 16 29 56 24 29 48
26 99 61 65 53 58 37 78 80 70 42 10 50 67 42 32 17 55 85 74 94 44 67 16 94
14 65 52 68 75 87 59 36 22 41 26 78 63 06 55 13 08 27 01 50 15 29 39 39 43
(2)若采用系统抽样法抽样,且样本中最小编号为08,求样本中所有编号之和:
(3)若采用分层轴样,按照学生选择![]() 题目或
题目或![]() 题目,将成绩分为两层,且样本中
题目,将成绩分为两层,且样本中![]() 题目的成绩有8个,平均数为7,方差为4:样本中
题目的成绩有8个,平均数为7,方差为4:样本中![]() 题目的成绩有2个,平均数为8,方差为1.用样本估计900名考生选做题得分的平均数与方差.
题目的成绩有2个,平均数为8,方差为1.用样本估计900名考生选做题得分的平均数与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0)的离心率e
1(a>b>0)的离心率e![]() ,且点P(
,且点P(![]() ,1)在椭圆C上.
,1)在椭圆C上.
(1)求椭圆C的方程;
(2)若椭圆C的左焦点为F,右顶点为A,点M(s,t)(t>0)是椭圆C上的动点,直线AM与y轴交于点D,点E是y轴上一点,EF⊥DF,EA与椭圆C交于点G,若△AMG的面积为2![]() ,求直线AM的方程.
,求直线AM的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月25日-27日,北京召开第二届“一带一路”国际高峰论坛,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这三个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数为 ( )
A. 198B. 268C. 306D. 378
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点O与直角坐标系的原点重合,极轴与直角坐标系中x轴的正半轴重合.圆C的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),直线l:
),直线l:![]() ,若直线l与曲线C相交于A,B两点,且
,若直线l与曲线C相交于A,B两点,且![]() .
.
(1)求a;
(2)若M,N为曲线C上的两点,且![]() ,求
,求![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,ABCD为矩形,
中,ABCD为矩形,![]() 是以
是以![]() 为直角的等腰直角三角形,平面
为直角的等腰直角三角形,平面![]() 平面ABCD.
平面ABCD.

(1)证明:平面![]() 平面PBC;
平面PBC;
(2)![]() 为直线PC的中点,且
为直线PC的中点,且![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com