
【题目】已知函数![]() (
(![]() ,
,![]() 是自然对数的底数).
是自然对数的底数).
(1)若![]() 是
是![]() 上的单调递增函数,求实数
上的单调递增函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,证明:函数
时,证明:函数![]() 有最小值,并求函数
有最小值,并求函数![]() 最小值的取值范围.
最小值的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析: (Ⅰ)先将单调性转化为不等式恒成立:当![]() 时,函数
时,函数![]() 恒成立,再变量分离转化为对应函数最值:
恒成立,再变量分离转化为对应函数最值:![]() 的最小值,最后根据导数求函数
的最小值,最后根据导数求函数![]() 最值,(Ⅱ)利用二次求导,确定导函数为单调递增函数,再利用零点存在定理确定导函数有且仅有一个零点,根据导函数符号变化规律得函数在此零点(极小值点)取最小值.最后利用导函数零点表示函数最小值,并根据导函数零点取值范围,利用导数方法确定最小值函数的值域.
最值,(Ⅱ)利用二次求导,确定导函数为单调递增函数,再利用零点存在定理确定导函数有且仅有一个零点,根据导函数符号变化规律得函数在此零点(极小值点)取最小值.最后利用导函数零点表示函数最小值,并根据导函数零点取值范围,利用导数方法确定最小值函数的值域.
试题解析: (Ⅰ)![]() ,
,
依题意:当![]() 时,函数
时,函数![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
记![]() ,则
,则![]()
![]() ,
,
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,所以
,所以![]() ,即
,即![]() ;
;
(Ⅱ)因为![]() ,所以
,所以![]() 是
是![]() 上的增函数,
上的增函数,
又![]() ,
,![]() ,所以存在
,所以存在![]() 使得
使得![]()
且当![]() 时
时![]() ,当
,当![]() 时
时![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.
又当![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() .且有
.且有![]()
∴![]() .
.
记![]() ,则
,则![]()
![]() ,
,
所以![]() ,即最小值的取值范围是
,即最小值的取值范围是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)在R上是单调递减的一次函数,且f(f(x))=4x-1.
(1)求f(x);
(2)求函数y=f(x)+x2-x在x∈[-1,2]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地方政府要将一块如图所示的直角梯形ABCD空地改建为健身娱乐广场.已知AD//BC, ![]() 百米,
百米, ![]() 百米,广场入口P在AB上,且
百米,广场入口P在AB上,且![]() ,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),
,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),![]() 区域拟建为跳舞健身广场,
区域拟建为跳舞健身广场, ![]() 区域拟建为儿童乐园,其它区域铺设绿化草坪,设
区域拟建为儿童乐园,其它区域铺设绿化草坪,设![]() .
.
(1)求绿化草坪面积的最大值;
(2)现拟将两条小路PNM,PN进行不同风格的美化,PM小路的美化费用为每百米1万元,PN小路的美化费用为每百米2万元,试确定M,N的位置,使得小路PM,PN的美化总费用最低,并求出最小费用.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1: ![]() (t为参数)曲线C2:
(t为参数)曲线C2:![]() +y2=4.
+y2=4.
(1)在同一平面直角坐标系中,将曲线C2上的点按坐标变换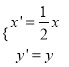 后得到曲线C′。求曲线C′的普通方程,并写出它的参数方程;
后得到曲线C′。求曲线C′的普通方程,并写出它的参数方程;
(2)若C1上的点P对应的参数为t=π/2,Q为C′上的动点,求PQ中点M到直线C3: ![]() (t为参数)的距离的最小值
(t为参数)的距离的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() .若直线
.若直线![]() 与圆C相交于不同的两点P,Q.
与圆C相交于不同的两点P,Q.
(Ⅰ)写出圆C的直角坐标方程,并求圆心的坐标与半径;
(Ⅱ)若弦长|PQ|=4,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个正数a,b,可按规则![]() 扩充为一个新数c,在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
扩充为一个新数c,在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
(1)若a=1,b=3,按上述规则操作三次,扩充所得的数是_____________;
(2)若p>q>0,经过6次操作后扩充所得的数为![]() (m,n为正整数),
(m,n为正整数),
则m,n的值分别为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com