
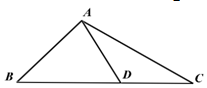
 如图,在△ABC中,∠B=45°,D是BC边上一点,AB=$\frac{5}{2}\sqrt{6}$,AC=5$\sqrt{3}$,AD=5,∠ADB为锐角.
如图,在△ABC中,∠B=45°,D是BC边上一点,AB=$\frac{5}{2}\sqrt{6}$,AC=5$\sqrt{3}$,AD=5,∠ADB为锐角.分析 (1)在三角形ADB中,利用正弦定理表示出sin∠ADB,求出∠ADB,确定出∠ADC的度数;
(2)在△ADC中,设CD=x,由余弦定理可得,AC2=AD2+CD2-2AD•CD•cos∠ADC即可求出CD的长.
解答 解:(1)在△ABC中,∵$∠B={45°},AB=\frac{{5\sqrt{6}}}{2}$,
∴由正弦定理可得,$\frac{AB}{sin∠ADB}=\frac{AD}{sin∠B}$QUOTE,即$\frac{{\frac{{5\sqrt{6}}}{2}}}{sin∠ADB}=\frac{5}{{sin{{45}°}}}$,…(2分)
E∴$sin∠ADB=\frac{{\sqrt{3}}}{2}$,∵∠ADB为锐角,∴∠ADB=60°.…(4分)∴∠ADC=120°.…(5分)
(2)在△ADC中,设CD=x,由余弦定理可得,AC2=AD2+CD2-2AD•CD•cos∠ADC…(7分)
∴${(5\sqrt{3})^2}={5^2}+C{D^2}-2×5•CD•cos∠{120°}$,即x2+5x-50=0,…(9分)
(x+10)(x-5)=0,∴x=5,即CD=5.…(10分)
点评 考查了正弦、余弦定理,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -sin1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?{x_0}∈R,{e^{x_0}}>{x_0}$ | B. | ?x∈R,ex<x | ||
| C. | ?x∈R,ex≤x | D. | $?{x_0}∈R,{e^{x_0}}≤{x_0}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=-\frac{1}{8}$ | B. | $y=-\frac{1}{8}$ | C. | $y=-\frac{1}{4}$ | D. | $y=-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,$\frac{1}{3}$] | C. | (0,$\frac{1}{6}$) | D. | ($\frac{1}{6}$,$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
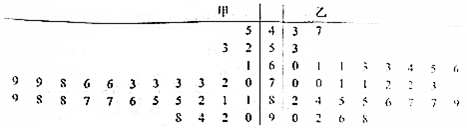
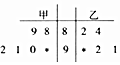 在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6位选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图.为了增加结果的神秘感,主持人暂时没有公布甲、乙两班最好一位选手的成绩.
在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6位选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图.为了增加结果的神秘感,主持人暂时没有公布甲、乙两班最好一位选手的成绩.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com