
【题目】在△ABC中,D在AB上,AD:DB=1:2,E为AC中点,CD、BE相交于点P,连结AP.设 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R),则x,y的值分别为( )
(x,y∈R),则x,y的值分别为( )
A.![]()
B.![]()
C.![]()
D.![]()
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,横、纵坐标均为整数的点叫做格点.若函数y=f(x)的图象恰好经过k个格点,则称函数y=f(x)为k阶格点函数.已知函数:①y=x2;②y=2sinx,③y=πx﹣1;④y=cos(x+ ![]() ).其中为一阶格点函数的序号为(注:把你认为正确论断的序号都填上)
).其中为一阶格点函数的序号为(注:把你认为正确论断的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为 ![]() (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ. (Ⅰ)把C1的参数方程化为极坐标方程;
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ. (Ⅰ)把C1的参数方程化为极坐标方程;
(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2, ![]() cos2B+5cosB﹣
cos2B+5cosB﹣ ![]() =0,且点D在线段BC上.
=0,且点D在线段BC上. 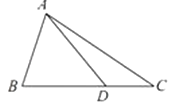
(1)若∠ADC= ![]() ,求AD的长;
,求AD的长;
(2)若BD=2DC, ![]() =4
=4 ![]() ,求△ABD的面积.
,求△ABD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和 ![]() ,数列{bn}的前n项和为Bn .
,数列{bn}的前n项和为Bn .
(1)求数列{an}的通项公式;
(2)设 ![]() ,求数列{cn}的前n项和Cn;
,求数列{cn}的前n项和Cn;
(3)证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的左、右焦点为F1 , F2 , 设点F1 , F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
=1(a>b>0)的左、右焦点为F1 , F2 , 设点F1 , F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
(1)求椭圆C的标准方程;
(2)设A,B,P为椭圆C上三点,满足 ![]() =
= ![]()
![]() +
+ ![]()
![]() ,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M,N两点,求|MN|.
,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M,N两点,求|MN|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com