Question

17．已知定义在R上的函数f（x）满足f（x+3）-f（x）=0，且f（x）=$\left\{\begin{array}{l}{-{x}^{2}+1，-1≤x≤1}\\{lo{g}_{2}x，1＜x＜2}\end{array}\right.$，若函数y=f（x）-$\frac{t}{3}$x（t＞0）至少有9个零点，则t的取值范围为（　　）

• A． （0，$\frac{1}{3}$）
• B． （0，54-24$\sqrt{5}$]
• C． （0，$\frac{1}{2}$）
• D． （0，$\frac{1}{3}$]

Answer 1

分析 函数f（x）满足f（x+3）-f（x）=0，得周期T=3，函数y=f（x）-$\frac{t}{3}$x（t＞0）的零点，就是y=f（x ）与y=$\frac{t}{3}x$的交点，作出两个函数的图象，利用图象确定函数零点的个数，求出t的取值范围．

解答 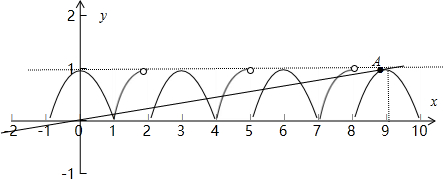解：∵定义在R上的函数f（x）满足f（x+3）-f（x）=0，∴周期T=3
画出函数f（x）在[-1，10]的图象，如图所示，当直线y=$\frac{t}{3}x$相切于点A（x₀，y₀）时刚好9个零点，
当x∈（8，10）时，f（x）=-（x-9）²+1，所以过点A的切线方程为y-y₀=-2（x₀-9）（x-x₀）
∵切线过原点，-y₀=-2（x₀-9）（-x₀），又∵y₀=-（x₀-9）²+1，解得x₀=4$\sqrt{5}$，
，$\frac{t}{3}$=f′（x）=-2（x-9）=18-8$\sqrt{5}$
，t的取值范围为（0，54-24$\sqrt{5}$]
故选：B．

点评 本题考查了函数零点的个数判定，利用零点定义将函数转化为两个基本初等函数，数形结合是关键，属于难题．