练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列命题中,错误的是()

    A. 一条直线与两个平行平面中的一个相交, 则必与另一个平面相交

    B. 平行于同一平面的两个不同平面平行

    C. 若直线不平行平面, 则在平面内不存在与平行的直线

    D. 如果平面不垂直平面, 那么平面内一定不存在直线垂直于平面

    【答案】C

    【解析】由直线与平面相交的性质，知一条直线与两个平行平面中的一个相交，则必与另一个平面相交，故A正确；

    由平面平行的判定定理知，平行于同一平面的两个不同平面平行，故B正确；

    若直线l不平行平面α，则当lα时，在平面α内存在与l平行的直线，故C不正确；

    由直线与平面垂直的性质定理，知如果平面α不垂直平面β，那么平面α内一定不存在直线垂直于平面β，故D正确。

    本题选择C选项.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数，其中a为常数．

    Ⅰ当，求a的值；

    Ⅱ当时，关于x的不等式恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.其中表示的导函数在的取值．

    (1)求的值及函数的单调区间；

    (2)若在的定义域内恒成立，求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求该函数的定义域；

    （2）当时，如果对任何都成立，求实数的取值范围；

    （3）若，将函数的图像沿轴方向平移，得到一个偶函数的图像，设函数的最大值为，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业为确定下一年投入某种产品的研发费用，需了解年研发费用（单位：千万元）对年销售量（单位：千万件）的影响，统计了近年投入的年研发费用与年销售量的数据，得到散点图如图所示．

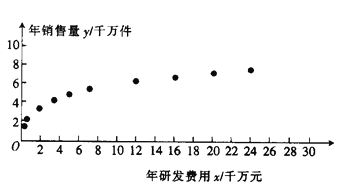
    (1)利用散点图判断和（其中均为大于的常数）哪一个更适合作为年销售量和年研发费用的回归方程类型（只要给出判断即可，不必说明理由）

    (2)对数据作出如下处理，令，得到相关统计量的值如下表：根据第(1)问的判断结果及表中数据，求关于的回归方程；

    15

    15

    28.25

    56.5

    (3)已知企业年利润（单位：千万元）与的关系为（其中），根据第(2)问的结果判断，要使得该企业下一年的年利润最大，预计下一年应投入多少研发费用?

    附：对于一组数据，其回归直线的斜率和截距的最小二乘估计分别为，

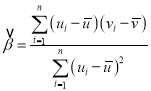    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若数列同时满足：①对于任意的正整数， 恒成立；②对于给定的正整数， 对于任意的正整数恒成立，则称数列是“数列”.

    （1）已知判断数列是否为“数列”，并说明理由；

    （2）已知数列是“数列”，且存在整数，使得， ， ， 成等差数列，证明： 是等差数列.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）若函数在上是增函数，求实数的取值范围；

    （2）若存在实数使得关于的方程有三个不相等的实数根，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正项数列，满足：对任意正整数，都有，，成等差数列，，，成等比数列，且，．

    （Ⅰ）求证：数列是等差数列；

    （Ⅱ）求数列，的通项公式；

    （Ⅲ）设=++…+，如果对任意的正整数，不等式恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若是的导函数，讨论的单调性；

    （2）若（是自然对数的底数），求证：.

    查看答案和解析>>

    同步练习册答案