
【题目】某工厂的检验员为了检测生产线上生产零件的情况,从产品中随机抽取了![]() 个进行测量,根据所测量的数据画出频率分布直方图如下:
个进行测量,根据所测量的数据画出频率分布直方图如下:
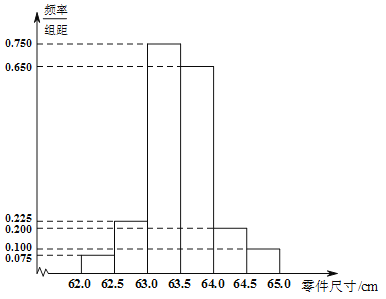
注:尺寸数据在![]() 内的零件为合格品,频率作为概率.
内的零件为合格品,频率作为概率.
(Ⅰ) 从产品中随机抽取![]() 件,合格品的个数为
件,合格品的个数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(Ⅱ) 从产品中随机抽取![]() 件,全是合格品的概率不小于
件,全是合格品的概率不小于![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ) 为了提高产品合格率,现提出![]() 两种不同的改进方案进行试验.若按
两种不同的改进方案进行试验.若按![]() 方案进行试验后,随机抽取
方案进行试验后,随机抽取![]() 件产品,不合格个数的期望是
件产品,不合格个数的期望是![]() ;若按
;若按![]() 方案试验后,抽取
方案试验后,抽取![]() 件产品,不合格个数的期望是
件产品,不合格个数的期望是![]() ,你会选择哪个改进方案?
,你会选择哪个改进方案?
【答案】(Ⅰ)分布列见解析,![]() ; (Ⅱ)
; (Ⅱ)![]() ; (Ⅲ)选择方案
; (Ⅲ)选择方案![]() .
.
【解析】
(Ⅰ)先根据直方图求出合格率,然后求出ξ的可能取值和相应的概率,作分布列,再利用随机变量的分布列进行求期望;
(Ⅱ)根据n件产品都合格的概率大于等于0.3,列不等式求解n的最大值;
(Ⅲ)根据期望求出A,B方案不合格的概率,即可选择.
(Ⅰ)由直方图可知,抽出产品为合格品的频率为![]() ,即抽出产品为合格品的概率为
,即抽出产品为合格品的概率为![]() , 从产品中随机抽取
, 从产品中随机抽取![]() 件,合格品的个数
件,合格品的个数![]() 的所有可能取值为
的所有可能取值为![]() 且
且 ![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() , 所以
, 所以![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
|
|
故数学期望![]()
![]()
![]()
(Ⅱ) 随机抽取![]() 件,全是合格品的概率为
件,全是合格品的概率为![]() ,依题意
,依题意![]() ,故
,故![]() 的最大值为
的最大值为![]() .
.
(Ⅲ) 按![]() 方案随机抽取产品不合格的概率是
方案随机抽取产品不合格的概率是![]() ,随机抽取
,随机抽取![]() 件产品,不合格个数
件产品,不合格个数![]() ;
;
按![]() 方案随机抽取产品不合格的概率是
方案随机抽取产品不合格的概率是![]() ,随机抽取
,随机抽取![]() 件产品,不合格个数
件产品,不合格个数![]() ,
,
依题意![]() ,
,![]() ,解得
,解得![]() ,
,
因为![]() ,所以应选择方案
,所以应选择方案![]() .
.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为F1,F2,离心率
的左、右焦点分别为F1,F2,离心率![]() ,且椭圆的短轴长为2.
,且椭圆的短轴长为2.
(1)求椭圆的标准方程;
(2)已知直线l1,l2过右焦点F2,且它们的斜率乘积为﹣1,设l1,l2分别与椭圆交于点A,B和C,D.①求AB+CD的值;②设AB的中点M,CD的中点为N,求△OMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次考试中500名学生的物理(满分为150分)成绩服从正态分布![]() ,数学成绩的频率分布直方图如图所示.
,数学成绩的频率分布直方图如图所示.

(Ⅰ)如果成绩大于135分为特别优秀,那么本次考试中的物理、数学特别优秀的大约各有多少人?
(Ⅱ)如果物理和数学两科都特别优秀的共有4人,是否有99.9%的把握认为物理特别优秀的学生,数学也特别优秀?
附:①若![]() ,则
,则![]()
②表及公式:
| 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形ABCD的边长为2,AC∩BD=O.将正方形ABCD沿对角线BD折起,使AC=a,得到三棱锥A-BCD,如图所示.

(1)当a=2时,求证:AO⊥平面BCD.
(2)当二面角A-BD-C的大小为120°时,求二面角A-BC-D的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推进“千村百镇计划”,2019年4月某新能源公司开展“电动绿色出行”活动,首批投放200台![]() 型新能源车到某地多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对
型新能源车到某地多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对![]() 型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为100分).最后该公司共收回有效评分表600份,现从中随机抽取40份(其中男、女的评分表各20份)作为样本,经统计得到茎叶图:
型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为100分).最后该公司共收回有效评分表600份,现从中随机抽取40份(其中男、女的评分表各20份)作为样本,经统计得到茎叶图:
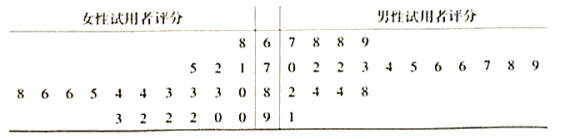
(1)求40个样本数据的中位数![]() ;
;
(2)已知40个样本数据的平均数![]() ,记
,记![]() 与
与![]() 的最大值为
的最大值为![]() .该公司规定样本中试用者的“认定类型”:评分不小于
.该公司规定样本中试用者的“认定类型”:评分不小于![]() 的为“满意型”,评分小于
的为“满意型”,评分小于![]() 的为“需改进型”.
的为“需改进型”.
①请以40个样本数据的频率分布来估计收回的600份评分表中,评分小于![]() 的份数;
的份数;
②请根据40个样本数据,完成下面2×2列联表:
认定类型 性别 | 满意型 | 需改进型 | 合计 |
女性 | 20 | ||
男性 | 20 | ||
合计 | 40 |
根据2×2列联表判断能否有99%的把握认为“认定类型”与性别有关?
附: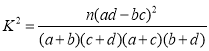 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)如果把棱柱中过不相邻的两条侧棱的截面叫棱柱的“对角面”,则平行六面体的对角面的形状是_______,直平行六面体的对角面的形状是______;
(2)过正三棱柱底面的一边和两底面中心连线段的中点作截面,则这个截面的形状为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.

(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com