
【题目】已知函数![]() .
.
(1)令![]() ,判断g(x)的单调性;
,判断g(x)的单调性;
(2)当x>1时,![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)求出![]() ,分两种情况讨论
,分两种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)讨论
的减区间;(2)讨论![]() 的范围,分别利用导数以及函数的单调性,结合单调性判断函数
的范围,分别利用导数以及函数的单调性,结合单调性判断函数![]() 是否有最大值,当函数
是否有最大值,当函数![]() 有最大值时,令其最大值小于零即可求得
有最大值时,令其最大值小于零即可求得![]() 的范围.
的范围.
(1)由![]() ,则
,则![]() ,
,
所以![]() (x>0).
(x>0).
①当a≤0时,![]() ,
,![]() 为
为![]() 的减函数;
的减函数;
②当a>0时,
若![]() ,即
,即![]() 时,
时,![]() ,
,![]() 为
为![]() 的减函数;
的减函数;
若![]() ,即
,即![]() 时,由
时,由![]() 有两根
有两根![]() 得
得
在![]() 上
上![]() ,
,![]() 为减函数;在
为减函数;在![]() 上
上![]() ,
,![]() 为增函数;
为增函数;
在![]() 上
上![]() ,
,![]() 为减函数.
为减函数.
综上:当![]() 时,
时,![]() 为
为![]() 的减函数;
的减函数;
当![]() 时,在
时,在![]() 上
上![]() ,
,![]() 为减函数;在
为减函数;在![]() 上
上![]() ,
,![]() 为增函数;在
为增函数;在![]() 上
上![]() ,
,![]() 为减函数.
为减函数.
(2)由(1)知,对a讨论如下,
①当a≤0时,![]() ,则
,则![]() 为(1,+∞)上的减函数,
为(1,+∞)上的减函数,
则![]() ,故
,故![]() 为(1,+∞)的减函数,
为(1,+∞)的减函数,
由于![]() ,所以
,所以![]() ,即a≤0时满足题意.
,即a≤0时满足题意.
②当a>0时,由于![]() ,对其讨论如下:
,对其讨论如下:
(A)若![]() ,即a≤1,则由(1)知,
,即a≤1,则由(1)知,![]() 为(1,+∞)上的减函数,
为(1,+∞)上的减函数,
则![]() ,所以
,所以![]() 为(1,+∞)的减函数,
为(1,+∞)的减函数,
由于![]() ,所以
,所以![]() ,即0<a≤1时满足题意.
,即0<a≤1时满足题意.
(B)若![]() ,即a>1,则由(1)知,
,即a>1,则由(1)知,
当![]() 时,
时,![]() 为(1,+∞)上的减函数,又
为(1,+∞)上的减函数,又![]() ,
,
所以存在![]() ,使得在
,使得在![]() 时,
时,![]() ,于是
,于是![]() 为
为![]() 的增函数,
的增函数,
因为![]() ,
,
所以![]() ,即1<a≤
,即1<a≤![]() 时不满足题意.
时不满足题意.
当![]() 时,由于
时,由于![]() ,所以对
,所以对![]() 与1的大小关系讨论如下,
与1的大小关系讨论如下,
1)如果![]() ,即
,即![]() ,那么由(1)知,
,那么由(1)知,![]() 为(1,+∞)上的减函数,
为(1,+∞)上的减函数,
又![]() ,
,
则存在![]() ,使得在
,使得在![]() 时,
时,![]() ,于是
,于是![]() 为
为![]() 的增函数,
的增函数,
又![]() ,则
,则![]() ,即
,即![]() 时不满足题意.
时不满足题意.
2)如果![]() ,即
,即![]() ,那么由(1)知,
,那么由(1)知,![]() 为(1,
为(1,![]() )上的增函数,
)上的增函数,
则当![]() 时,
时,![]() ,于是
,于是![]() 为
为![]() 的增函数,
的增函数,
又![]() ,则
,则![]() ,即
,即![]() 时不满足题意.
时不满足题意.
综上所述,a的取值范围为![]() .
.


 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
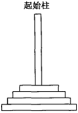
【题目】如图所示,在著名的汉诺塔问题中,有三根高度相同的柱子和一些大小及颜色各不相同的圆盘,三根柱子分别为起始柱、辅助柱及目标柱.已知起始柱上套有![]() 个圆盘,较大的圆盘都在较小的圆盘下面.现把圆盘从起始柱全部移到目标柱上,规则如下:每次只能移动一个圆盘,且每次移动后,每根柱上较大的圆盘不能放在较小的圆盘上面,规定一个圆盘从任一根柱上移动到另一根柱上为一次移动.若将
个圆盘,较大的圆盘都在较小的圆盘下面.现把圆盘从起始柱全部移到目标柱上,规则如下:每次只能移动一个圆盘,且每次移动后,每根柱上较大的圆盘不能放在较小的圆盘上面,规定一个圆盘从任一根柱上移动到另一根柱上为一次移动.若将![]() 个圆盘从起始柱移动到目标柱上最少需要移动的次数记为
个圆盘从起始柱移动到目标柱上最少需要移动的次数记为![]() ,则
,则![]() __________,
__________,![]() __________.
__________.
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数有( )
①向量![]() 与
与![]() 是共线向量,则A、B、C、D四点必在一直线上;②单位向量都相等;③任一向量与它的相反向量不相等;④共线的向量,若起点不同,则终点一定不同.
是共线向量,则A、B、C、D四点必在一直线上;②单位向量都相等;③任一向量与它的相反向量不相等;④共线的向量,若起点不同,则终点一定不同.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数fn(x)=xn+bx+c(n∈Z,b,c∈R).
(1)若n=﹣1,且f﹣1(1)=f﹣1(![]() )=5,试求实数b,c的值;
)=5,试求实数b,c的值;
(2)设n=2,若对任意x1,x2∈[﹣1,1]有|f2(x1)﹣f2(x2)|≤6恒成立,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com