
【题目】如图所示,在四棱锥P—ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.
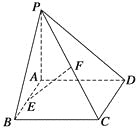
求证:(1)CD⊥PD;(2)EF⊥平面PCD.
【答案】(1)见解析;(2)见解析.
【解析】
试题1)证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的底边上的高,中线和顶角的角平分线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形等等; (2)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.
试题解析:(1)∵PA⊥底面ABCD,![]() 平面ABCD
平面ABCD
∴CD⊥PA.
又矩形ABCD中,CD⊥AD,
∵AD∩PA=A,![]() 平面PAD,
平面PAD,![]() 平面PAD
平面PAD
∴CD⊥平面PAD,
![]() 平面PAD∴CD⊥PD.
平面PAD∴CD⊥PD.
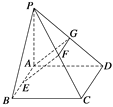
(2)取PD的中点G,连结AG,FG.又∵G、F分别是PD、PC的中点,
∴![]()
∴![]()
∴四边形AEFG是平行四边形,
∴AG∥EF.
∵PA=AD,G是PD的中点,
∴AG⊥PD,∴EF⊥PD,
∵CD⊥平面PAD,AG平面PAD.
∴CD⊥AG.∴EF⊥CD.
∵PD∩CD=D,![]() 平面PCD,CD
平面PCD,CD![]() 平面PCD
平面PCD
∴EF⊥平面PCD.


科目:高中数学 来源: 题型:
【题目】下列各组函数中,表示同一个函数的是( ).
A.y=x+1和y=![]() B.y=x0和y=
B.y=x0和y=![]() C.f(x)=(x-1)2和g(x)=(x+1)2D.f(x)=
C.f(x)=(x-1)2和g(x)=(x+1)2D.f(x)=![]() 和g(x)=
和g(x)=![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题10分) 从3名男生和![]() 名女生中任选2人参加比赛。
名女生中任选2人参加比赛。
①求所选2人都是男生的概率;
②求所选2人恰有1名女生的概率;
③求所选2人中至少有1名女生的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是实数,
是实数,![]() ,
,
(1)若函数![]() 为奇函数,求
为奇函数,求![]() 的值;
的值;
(2)试用定义证明:对于任意![]() ,
,![]() 在
在![]() 上为单调递增函数;
上为单调递增函数;
(3)若函数![]() 为奇函数,且不等式
为奇函数,且不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全集U=R,若集合A={x|2≤x<9},B={x|1<x≤6}.
(1)求(CRA)∪B;
(2)若集合C={x|a<x≤2a+7},且AC,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某体育用品商场经营一批进价为40元的运动服,经市场调查发现销售量y(件)与销售单价x(元)符合一次函数模型,且销售单价为60元时,销量是600件;当销售单价为64元时,销量是560件.
(1)写出销售量y(件)与销售单价x(元)之间的函数关系式![]() ;
;
(2)试求销售利润z(元)与销售单价x(元)之间的函数关系式;
(3)在(1)(2)条件下,当销售单价为多少元时,商场能获得最大利润?并求出此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(I)若曲线![]() ,参数方程为:
,参数方程为:![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程
的普通方程
(Ⅱ)若曲线![]() ,参数方程为
,参数方程为![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() ,与曲线
,与曲线![]() 交点分别为
交点分别为![]() ,求
,求![]() 的取值范围,
的取值范围,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com