
【题目】已知函数![]() .
.
(1)若![]() 在定义域上不单调,求
在定义域上不单调,求![]() 的取值范围;
的取值范围;
(2)设![]() 分别是
分别是![]() 的极大值和极小值,且
的极大值和极小值,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:由已知![]() ,
,
(1)①若![]() 在定义域上单调递增,讨论可得
在定义域上单调递增,讨论可得![]() ;②若
;②若![]() 在定义域上单调递减,讨论可得
在定义域上单调递减,讨论可得![]() .据此可得
.据此可得![]() .
.
(2)由(1)知,![]() .令
.令![]() 的两根分别为
的两根分别为![]() ,设
,设![]() ,则
,则![]() ,计算可得
,计算可得![]() 令
令![]() ,换元讨论可得
,换元讨论可得![]() .
.
详解:由已知![]() ,
,
(1)①若![]() 在定义域上单调递增,则
在定义域上单调递增,则![]() ,即
,即![]() 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
而![]() ,所以
,所以![]() ;
;
②若![]() 在定义域上单调递减,则
在定义域上单调递减,则![]() ,即
,即![]() 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
而![]() ,所以
,所以![]() .
.
因为![]() 在定义域上不单调,所以
在定义域上不单调,所以![]() ,即
,即![]() .
.
(2)由(1)知,欲使![]() 在(0,+∞)有极大值和极小值,必须
在(0,+∞)有极大值和极小值,必须![]() .
.
又![]() ,所以
,所以![]() .
.
令![]() 的两根分别为
的两根分别为![]() ,
,
即![]() 的两根分别为
的两根分别为![]() ,于是
,于是![]() .
.
不妨设![]() ,
,
则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,
,
所以![]()
![]()
![]()
令![]() ,于是
,于是![]() .
.
![]() ,
,
由![]() ,得
,得![]() .
.
因为![]() ,
,
所以![]() 在
在![]() 上为减函数.
上为减函数.
所以![]() .
.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() 到两点
到两点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,设点
,设点![]() 的轨迹为
的轨迹为![]() 。
。
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于点
交于点![]() 、
、![]() ,以线段
,以线段![]() 为直径的圆能否过坐标原点,若能,求出直线
为直径的圆能否过坐标原点,若能,求出直线![]() 的方程,若不能请说明理由.
的方程,若不能请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族![]() 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当![]() 中
中![]() (
(![]() )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为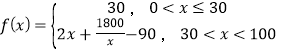 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为
影响,恒为![]() 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;讨论
的表达式;讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且x≤0时, f(x)=-x+1
(1)求f(0),f(2);
(2)求函数f(x)的解析式;
(3)若f(a-1)<3,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .若将
.若将![]() ,
, ![]() 分别沿
分别沿![]() 折起,使
折起,使![]() 两点重合于点
两点重合于点![]() ,如图2.
,如图2.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有![]() ,
,![]() 两个分厂生产某种产品,规定该产品的某项质量指标值不低于130的为优质品.分别从
两个分厂生产某种产品,规定该产品的某项质量指标值不低于130的为优质品.分别从![]() ,
,![]() 两厂中各随机抽取100件产品统计其质量指标值,得到如图频率分布直方图:
两厂中各随机抽取100件产品统计其质量指标值,得到如图频率分布直方图:
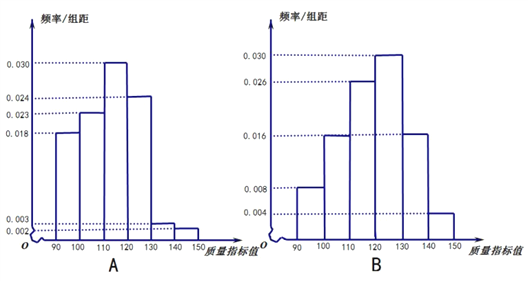
(1)根据频率分布直方图,分别求出![]() 分厂的质量指标值的众数和中位数的估计值;
分厂的质量指标值的众数和中位数的估计值;
(2)填写![]() 列联表,并根据列联表判断是否有
列联表,并根据列联表判断是否有![]() 的把握认为这两个分厂的产品质量有差异?
的把握认为这两个分厂的产品质量有差异?
优质品 | 非优质品 | 合计 | |
| |||
| |||
合计 |
(3)(i)从![]() 分厂所抽取的100件产品中,利用分层抽样的方法抽取10件产品,再从这10件产品中随机抽取2件,已知抽到一件产品是优质品的条件下,求抽取的两件产品都是优质品的概率;
分厂所抽取的100件产品中,利用分层抽样的方法抽取10件产品,再从这10件产品中随机抽取2件,已知抽到一件产品是优质品的条件下,求抽取的两件产品都是优质品的概率;
(ii)将频率视为概率,从![]() 分厂中随机抽取10件该产品,记抽到优质品的件数为
分厂中随机抽取10件该产品,记抽到优质品的件数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com