
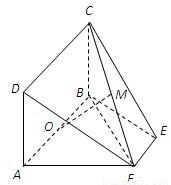
 ,底EF为1,再计算三棱锥C-BEF的高,即为CB,最后由三棱锥体积计算公式计算即可
,底EF为1,再计算三棱锥C-BEF的高,即为CB,最后由三棱锥体积计算公式计算即可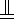
 CD,又AO
CD,又AO
 CD,则MN
CD,则MN AO,
AO,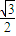 ,EF=AB-2HB=1,
,EF=AB-2HB=1, ×1×
×1×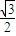 =
=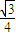
 ×S△BEF×BC=
×S△BEF×BC= ×
×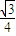 ×1=
×1=


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
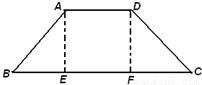
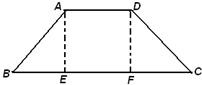 如图,等腰梯形ABCD中,E,F分别是BC上三等分点,AD=AE=1,BC=3,若把三角形ABE和DCF分别沿AE和DF折起,使得B、C两点重合于一点P,则二面角P-AD-E的大小为
如图,等腰梯形ABCD中,E,F分别是BC上三等分点,AD=AE=1,BC=3,若把三角形ABE和DCF分别沿AE和DF折起,使得B、C两点重合于一点P,则二面角P-AD-E的大小为
查看答案和解析>>
科目:高中数学 来源:2008-2009学年湖北省部分重点中学联考高二(下)期末数学试卷(理科)(解析版) 题型:填空题

查看答案和解析>>
科目:高中数学 来源:2011年宁夏固原一中高三适应性测试数学试卷3(文科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2009年北京市崇文区高考数学一模试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2009年北京市崇文区高考数学一模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com