
【题目】如图,在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() .点
.点![]() 、
、![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 、
、![]() 的中点,
的中点,![]() 是线段
是线段![]() 的中点,
的中点,![]() ,
,![]() .
.
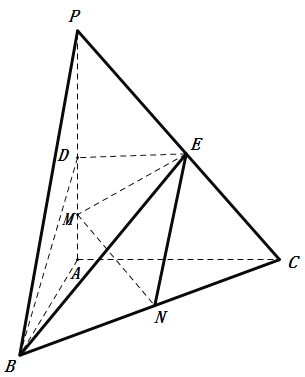
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)已知点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与直线
与直线![]() 所成角的余弦值为
所成角的余弦值为![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ;(3)4
;(3)4
【解析】
(1)取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,证明平面
,证明平面![]() 平面
平面![]() 得到答案.
得到答案.
(2)以![]() 为原点,分别以
为原点,分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系.平面
轴建立空间直角坐标系.平面![]() 的一个法向量为
的一个法向量为![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,计算夹角得到答案.
,计算夹角得到答案.
(3)设![]() ,则
,则![]() ,
,![]() ,
,![]() ,利用夹角公式计算得到答案.
,利用夹角公式计算得到答案.
(1)取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,∵
,∵![]() 为
为![]() 中点,∴
中点,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 为
为![]() 中点,∴
中点,∴![]() ,
,
又![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,∴
的中点,∴![]() ,则
,则![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴平面![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() .
.
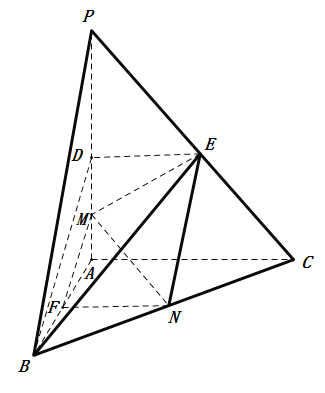
(2)∵![]() 底面
底面![]() ,
,![]() .
.
∴以![]() 为原点,分别以
为原点,分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由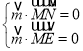 ,得
,得![]() ,取
,取![]() ,得
,得![]() .
.
由图可得平面![]() 的一个法向量为
的一个法向量为![]() .
.
∴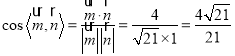 .
.
∴二面角![]() 的余弦值为
的余弦值为![]() ,则正弦值为
,则正弦值为![]() .
.
(3)设![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
∵直线![]() 与直线
与直线![]() 所成角的余弦值为
所成角的余弦值为![]() ,∴
,∴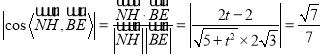 .
.
解得:![]() 或
或![]() (舍).
(舍).
∴当![]() 与
与![]() 重合时直线
重合时直线![]() 与直线
与直线![]() 所成角的余弦值为
所成角的余弦值为![]() ,此时线段
,此时线段![]() 的长为4.
的长为4.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知等比数列![]() 的首项
的首项![]() ,数列
,数列![]() 前
前![]() 项和记为
项和记为![]() ,前
,前![]() 项积记为
项积记为![]() .
.
(1) 若![]() ,求等比数列
,求等比数列![]() 的公比
的公比![]() ;
;
(2) 在(1)的条件下,判断![]() 与
与![]() 的大小;并求
的大小;并求![]() 为何值时,
为何值时,![]() 取得最大值;
取得最大值;
(3) 在(1)的条件下,证明:若数列![]() 中的任意相邻三项按从小到大排列,则总可以使其成等差数列;若所有这些等差数列的公差按从小到大的顺序依次记为
中的任意相邻三项按从小到大排列,则总可以使其成等差数列;若所有这些等差数列的公差按从小到大的顺序依次记为![]() ,则数列
,则数列![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 为坐标原点,C、D两点的坐标为
为坐标原点,C、D两点的坐标为![]() ,曲线
,曲线![]() 上的动点P满足
上的动点P满足![]() .又曲线
.又曲线![]() 上的点A、B满足
上的点A、B满足![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若点A在第一象限,且![]() ,求点A的坐标;
,求点A的坐标;
(3)求证:原点到直线AB的距离为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=log4(4x+1)+kx是偶函数.
(1)求k的值;
(2)判断函数y=f(x)-![]() x在R上的单调性,并加以证明;
x在R上的单调性,并加以证明;
(3)设g(x)=log4(a2x-![]() a),若函数f(x)与g(x)的图象有且仅有一个交点,求实数a的取值范围.
a),若函数f(x)与g(x)的图象有且仅有一个交点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线方程为![]() ,过其右焦点且斜率不为零的直线
,过其右焦点且斜率不为零的直线![]() 与双曲线交于A,B两点,直线
与双曲线交于A,B两点,直线![]() 的方程为
的方程为![]() ,A,B在直线
,A,B在直线![]() 上的射影分别为C,D.
上的射影分别为C,D.
(1)当![]() 垂直于x轴,
垂直于x轴,![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
(2)![]() ,
,![]() 的斜率为正实数,A在第一象限,B在第四象限,试比较
的斜率为正实数,A在第一象限,B在第四象限,试比较![]() 与1的大小;
与1的大小;
(3)是否存在实数![]() ,使得对满足题意的任意
,使得对满足题意的任意![]() ,直线
,直线![]() 和直线
和直线![]() 的交点总在
的交点总在![]() 轴上,若存在,求出所有的
轴上,若存在,求出所有的![]() 值和此时直线
值和此时直线![]() 和
和![]() 交点的位置;若不存在,请说明理由.
交点的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 满足:
满足:![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() .
.
① 记![]() ,求证:数列
,求证:数列![]() 为等差数列;
为等差数列;
② 若数列![]() 中任意一项的值均未在该数列中重复出现无数次,求首项
中任意一项的值均未在该数列中重复出现无数次,求首项![]() 应满足的条件.
应满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市三地A,B,C有直道互通.现甲交警沿路线AB乙交警沿路线ACB同时从A地出发,匀速前往B地进行巡逻,并在B地会合后再去执行其他任务.已知AB=10km,AC=6km,BC=8km,甲的巡逻速度为5km/h,乙的巡逻速度为10km/h.
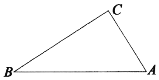
(1)求乙到达C地这一时刻的甲乙两交警之间的距离;
(2)已知交警的对讲机的有效通话距离不大于3km,从乙到达C地这一时刻算起,求经过多长时间,甲乙方可通过对讲机取得联系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
从数列![]() 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列![]() 的一个子数列.
的一个子数列.
设数列![]() 是一个首项为
是一个首项为![]() 、公差为
、公差为![]()
![]() 的无穷等差数列.
的无穷等差数列.
(1)若![]() ,
,![]() ,
,![]() 成等比数列,求其公比
成等比数列,求其公比![]() .
.
(2)若![]() ,从数列
,从数列![]() 中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为
中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为![]() 的无穷等比子数列,请说明理由.
的无穷等比子数列,请说明理由.
(3)若![]() ,从数列
,从数列![]() 中取出第1项、第
中取出第1项、第![]()
![]() 项(设
项(设![]() )作为一个等比数列的第1项、第2项,试问当且仅当
)作为一个等比数列的第1项、第2项,试问当且仅当![]() 为何值时,该数列为
为何值时,该数列为![]() 的无穷等比子数列,请说明理由.
的无穷等比子数列,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个特定时段内,以点E为中心的7n mile以内海域被设为警戒水域.点E正北55n mile处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40![]() n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东
n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东![]() (其中
(其中![]() ,
,![]() )且与点A相距10
)且与点A相距10![]() n mile的位置C.
n mile的位置C.
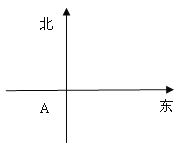
(I)求该船的行驶速度(单位:n mile /h);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com