
【题目】已知函数f(x)=Asin(x+ ![]() ),x∈R,且f(
),x∈R,且f( ![]() )=
)= ![]() .
.
(1)求A的值;
(2)若f(θ)+f(﹣θ)= ![]() ,θ∈(0,
,θ∈(0, ![]() ),求f(
),求f( ![]() ﹣θ).
﹣θ).
【答案】
(1)解:∵函数f(x)=Asin(x+ ![]() ),x∈R,且f(
),x∈R,且f( ![]() )=
)= ![]() .
.
∴Asin( ![]() +
+ ![]() )=Asin
)=Asin ![]() =A
=A ![]() =
= ![]() ,
,
∴A= ![]()
(2)解:由(1)可得 f(x)= ![]() sin(x+
sin(x+ ![]() ),
),
∴f(θ)+f(﹣θ)= ![]() sin(θ+
sin(θ+ ![]() )+
)+ ![]() sin(﹣θ+
sin(﹣θ+ ![]() )=2
)=2 ![]() sin
sin ![]() cosθ=
cosθ= ![]() cosθ=
cosθ= ![]() ,
,
∴cosθ= ![]() ,再由 θ∈(0,
,再由 θ∈(0, ![]() ),可得sinθ=
),可得sinθ= ![]() .
.
∴f( ![]() ﹣θ)=
﹣θ)= ![]() sin(
sin( ![]() ﹣θ+
﹣θ+ ![]() )=
)= ![]() sin(π﹣θ)=
sin(π﹣θ)= ![]() sinθ=
sinθ= ![]()
【解析】(1)由函数f(x)的解析式以及f( ![]() )=
)= ![]() ,求得A的值.(2)由(1)可得 f(x)=
,求得A的值.(2)由(1)可得 f(x)= ![]() sin(x+
sin(x+ ![]() ),根据f(θ)+f(﹣θ)=
),根据f(θ)+f(﹣θ)= ![]() ,求得cosθ 的值,再由 θ∈(0,
,求得cosθ 的值,再由 θ∈(0, ![]() ),求得sinθ 的值,从而求得f(
),求得sinθ 的值,从而求得f( ![]() ﹣θ) 的值.
﹣θ) 的值.


科目:高中数学 来源: 题型:
【题目】函数![]() 的一段图象过点
的一段图象过点![]() ,如图所示.
,如图所示.
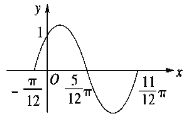
(1)求函数![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得函数
个单位,得函数![]() 的图象,求
的图象,求![]() 的最大值,并求出此时自变量
的最大值,并求出此时自变量![]() 的集合,并写出该函数的增区间.
的集合,并写出该函数的增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,﹣2),椭圆E: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,F是椭圆的焦点,直线AF的斜率为
,F是椭圆的焦点,直线AF的斜率为 ![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2002年北京国际数学家大会会标,是以中国古代数学家赵爽的弦图为基础而设计的,弦图用四个全等的直角三角形与一个小正方形拼成的一个大正方形![]() 如图
如图![]() ,若大、小正方形的面积分别为25和1,直角三角形中较大锐角为
,若大、小正方形的面积分别为25和1,直角三角形中较大锐角为![]() ,则
,则![]() 等于
等于![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的离心率为
的离心率为![]() ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为![]() .
.
(1)求双曲线C的方程;
(2)直线y=kx+m(k≠0, m≠0)与该双曲线C交于不同的两点C,D,且C,D两点都在以点A为圆心的同一圆上,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是 ( )
A. 某事件发生的概率为1.1 B. 对立事件也是互斥事件
C. 不能同时发生的的两个事件是两个对立事件 D. 某事件发生的概率是随着实验次数的变化而变化的
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中正确的是( )
① 如果一条直线不在某个平面内,那么这条直线就与这个平面平行;
② 过直线外一点有无数个平面与这条直线平行;
③ 过平面外一点有无数条直线与这个平面平行;
④ 过空间一点必存在某个平面与两条异面直线都平行.
A. ①④B. ②③C. ①②③D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国明代珠算家程大位的名著《直指算法统宗》中有如下问题:“今有白米一百八十石,令三人从上及和减率分之,只云甲多丙米三十六石,问:各该若干?”其意思为:“今有白米一百八十石,甲、乙、丙三人来分,他们分得的白米数构成等差数列,只知道甲比丙多分三十六石,那么三人各分得多少白米?”请问:乙应该分得( )白米
A. 96石B. 78石C. 60石D. 42石
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com