
【题目】在四棱锥![]() 中,
中,![]() 是等边三角形,点
是等边三角形,点![]() 在棱
在棱![]() 上,平面
上,平面![]() 平面
平面![]() .
.
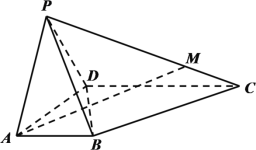
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值的最大值.
所成角的正弦值的最大值.
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】某科研团队对![]() 例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中
例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中![]() 名吸烟患者中,重症人数为
名吸烟患者中,重症人数为![]() 人,重症比例约为
人,重症比例约为![]() ;
;![]() 名非吸烟患者中,重症人数为
名非吸烟患者中,重症人数为![]() 人,重症比例为
人,重症比例为![]() .
.
(1)根据以上数据完成![]() 列联表;
列联表;
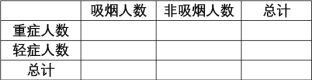
(2)根据(1)中列联表数据,能否在犯错误的概率不超过![]() 的前提下认为新冠肺炎重症与吸烟有关?
的前提下认为新冠肺炎重症与吸烟有关?
(3)已知每例重症患者平均治疗费用约为![]() 万元,每例轻症患者平均治疗费用约为
万元,每例轻症患者平均治疗费用约为![]() 万元.根据(1)中列联表数据,分别求吸烟患者和非吸烟患者的平均治疗费用.(结果保留两位小数)
万元.根据(1)中列联表数据,分别求吸烟患者和非吸烟患者的平均治疗费用.(结果保留两位小数)
附:
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平行四边形ABCD中,∠A![]() ,2AB=BC,E,F分别是BC,AD的中点.将四边形DCEF沿着EF折起,使得平面ABEF⊥平面DCEF,得到三棱柱AFD﹣BEC.
,2AB=BC,E,F分别是BC,AD的中点.将四边形DCEF沿着EF折起,使得平面ABEF⊥平面DCEF,得到三棱柱AFD﹣BEC.
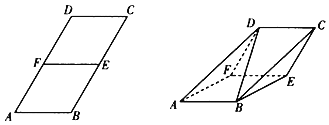
(1)证明:DB⊥EF;
(2)若AB=2,求三棱柱AFD﹣BEC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年新年伊始,新型冠状病毒来势汹汹,疫情使得各地学生在寒假结束之后无法返校,教育部就此提出了线上教学和远程教学,停课不停学的要求也得到了家长们的赞同.各地学校开展各式各样的线上教学,某地学校为了加强学生爱国教育,拟开设国学课,为了了解学生喜欢国学是否与性别有关,该学校对100名学生进行了问卷调查,得到如下列联表:
喜欢国学 | 不喜欢国学 | 合计 | |
男生 | 20 | 50 | |
女生 | 10 | ||
合计 | 100 |
(1)请将上述列联表补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为喜欢国学与性别有关系?
(2)针对问卷调查的100名学生,学校决定从喜欢国学的人中按分层抽样的方法随机抽取6人成立国学宣传组,并在这6人中任选2人作为宣传组的组长,设这两人中女生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
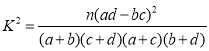 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校拟从甲、乙两名同学中选一人参加疫情知识问答竞赛,于是抽取了甲、乙两人最近同时参加校内竞赛的十次成绩,将统计情况绘制成如图所示的折线图.根据该折线图,下面结论正确的是( )
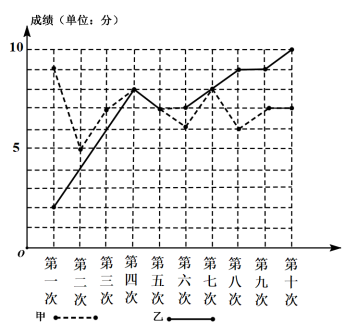
A.甲、乙成绩的中位数均为7
B.乙的成绩的平均分为6.8
C.甲从第四次到第六次成绩的下降速率要大于乙从第四次到第五次的下降速率
D.甲的成绩的方差小于乙的成绩的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com