
【题目】已知函数f(x)= ![]() 的定义域为集合A,函数g(x)=(
的定义域为集合A,函数g(x)=( ![]() )x(﹣1≤x≤0)的值域为集合B.
)x(﹣1≤x≤0)的值域为集合B.
(1)求A∩B;
(2)若集合C=[a,2a﹣1],且C∪B=B,求实数a的取值范围.
【答案】
(1)解:要使函数f(x)= ![]() 有意义,
有意义,
则log2(x﹣1)≥0,解得x≥2,
∴其定义域为集合A={x|x≥2}.
函数g(x)=( ![]() )x(﹣1≤x≤0)的值域为集合B={x|1≤x≤2},
)x(﹣1≤x≤0)的值域为集合B={x|1≤x≤2},
∴A∩B={2}
(2)解:∵C∪B=B,∴CB.
由题意2a﹣1>a,即a>1时,要使CB,则 ![]() ,
,
解得1<a≤ ![]()
【解析】(1)A是函数的定义域,只要解不等式log2(x﹣1)≥0即得,B是函数的值域,由指数函数的单调性可得;(2)条件C∪B=B,等价于CB,C是B的子集,即可求解.
【考点精析】根据题目的已知条件,利用集合的交集运算和函数的定义域及其求法的相关知识可以得到问题的答案,需要掌握交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立;求函数的定义域时,一般遵循以下原则:①
B,反之也成立;求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.


科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x),当x>0时,f(x)=﹣x2+2x
(1)求函数f(x)在R上的解析式;
(2)若函数f(x)在区间[﹣1,a﹣2]上单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集为R,集合A={x|﹣3≤x<6},B={x|2<x<9}.
(1)求A∩B,A∪(RB);
(2)已知C={x|a<x<2a+1},若CA,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() 的离心率是
的离心率是 ![]() ,其一条准线方程为x=
,其一条准线方程为x= ![]() .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)设双曲线C的左右焦点分别为A,B,点D为该双曲线右支上一点,直线AD与其左支交于点E,若 ![]() =λ
=λ ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A={x| ![]() <3x<9},B={x|log2x>0}.
<3x<9},B={x|log2x>0}.
(1)求A∩B和A∪B;
(2)定义A﹣B={x|x∈A且xB},求A﹣B和B﹣A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.,当每辆车的月租金定为x元时,租赁公司的月收益为y元,
(1)试写出x,y的函数关系式(不要求写出定义域);
(2)租赁公司某月租出了88辆车,求租赁公司的月收益多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在![]() 岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
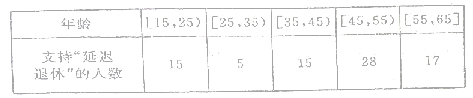
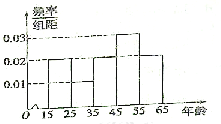
(1)由以上统计数据填![]() 列联表,并判断是否95%的把握认为以
列联表,并判断是否95%的把握认为以![]() 岁为界点的不同人群对“延迟退休年龄政策”的支持有差异;
岁为界点的不同人群对“延迟退休年龄政策”的支持有差异;

(2)若以![]() 岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取
岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取![]() 人参加某项活动,现从这
人参加某项活动,现从这![]() 人中随机抽
人中随机抽![]() 人.
人.
①抽到![]() 人是
人是![]() 岁以下时,求抽到的另一人是
岁以下时,求抽到的另一人是![]() 岁以上的概率;
岁以上的概率;
②记抽到![]() 岁以上的人数为
岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
|
|
|
|
|
|
|
|
|
|
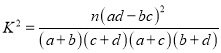
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示,并根据 
(1)写出函数f(x)(x∈R)的增区间;
(2)写出函数f(x)(x∈R)的解析式;
(3)若函数g(x)=f(x)﹣2ax+2(x∈[1,2]),求函数g(x)的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com