
【题目】已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为 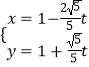 (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为 ![]() (α为参数),曲线C1上点P的极角为
(α为参数),曲线C1上点P的极角为 ![]() ,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(1)求椭圆的方程;
(2)若直线l与椭圆交于两点M,N(M,N不同于点A),若 ![]()
![]() =0,
=0, ![]() =
= ![]() ;
;
①求证:直线l过定点;并求出定点坐标;
②求直线AT的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )的最大值为
)的最大值为![]() ,最小值为
,最小值为![]() .
.
(1)求![]() 的值;
的值;
(2)将函数![]() 图象向右平移
图象向右平移![]() 个单位后,再将图象上所有点的纵坐标扩大到原来的
个单位后,再将图象上所有点的纵坐标扩大到原来的![]() 倍,横坐标不变,得到函数
倍,横坐标不变,得到函数![]() 的图象,求方程
的图象,求方程![]() 的解.
的解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点. 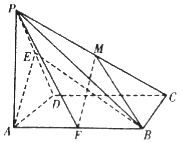
(1)求证:PD⊥平面ABE;
(2)若F为AB中点, ![]() ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为-
,试确定λ的值,使二面角P﹣FM﹣B的余弦值为- ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的方程为 ![]() +
+ ![]() =1(a>b>0),双曲线
=1(a>b>0),双曲线 ![]() ﹣
﹣ ![]() =1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4
=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4 ![]() .
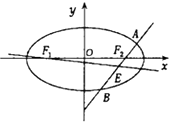
.
(1)求椭圆C的方程;
(2)设F1 , F2分别为椭圆C的左,右焦点,过F2作直线l(与x轴不重合)交于椭圆于A,B两点,线段AB的中点为E,记直线F1E的斜率为k,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a>0且a≠1,函数f(x)=![]() x2-(a+1)x+alnx.
x2-(a+1)x+alnx.
(1)当a=2时,求曲线y=f(x)在(3,f(3))处切线的斜率;
(2)求函数f(x)的极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() (
( ![]() 为常数,e=2.71828……是自然对数的底数).
为常数,e=2.71828……是自然对数的底数).
(1)当 ![]() 时,求函数
时,求函数 ![]() 的单调区间;
的单调区间;
(2)若函数 ![]() 在
在 ![]() 内存在两个极值点,求
内存在两个极值点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com