
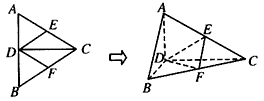
如图所示,AC为 的直径,D为
的直径,D为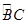 的中点,E为BC的中点.
的中点,E为BC的中点.

(Ⅰ)求证:AB∥DE;
(Ⅱ)求证:2AD·CD=AC·BC.
(Ⅰ)详见解析;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)通过连接BD,通过证明与同一条直线垂直的两条直线垂直的思路进行证明线线平行;(Ⅱ)通过证明△DAC∽△ECD,
试题解析:(Ⅰ)连接BD,因为D为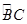 的中点,所以BD=DC.因为E为BC的中点,所以DE⊥BC.
的中点,所以BD=DC.因为E为BC的中点,所以DE⊥BC.
因为AC为圆的直径,所以∠ABC=90°,所以AB∥DE. 5分
(Ⅱ)因为D为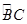 的中点,所以∠BAD=∠DAC,
的中点,所以∠BAD=∠DAC,
又∠BAD=∠DCB,则∠DAC=∠DCB.
又因为AD⊥DC,DE⊥CE,所以△DAC∽△ECD.
所以 =
= ,AD·CD=AC·CE,2AD·CD=AC·2CE,
,AD·CD=AC·CE,2AD·CD=AC·2CE,
因此2AD·CD=AC·BC. 10分

考点:1.线线平行的证明;2.三角形相似的证明.


科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
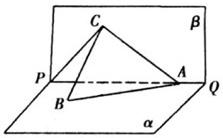 如图所示,PQ为平面α、β的交线,已知二面角α-PQ-β为直二面角,A∈PQ,B∈α,C∈β,CA=CB=kAB(k∈R*),∠BAP=45°.
如图所示,PQ为平面α、β的交线,已知二面角α-PQ-β为直二面角,A∈PQ,B∈α,C∈β,CA=CB=kAB(k∈R*),∠BAP=45°.
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源:北京模拟题 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖北省武汉二中高一(下)期末数学试卷(解析版) 题型:解答题
 时,求二面角B-AC-P的大小.
时,求二面角B-AC-P的大小.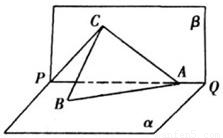
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省台州市高三(上)期末数学试卷(文科)(解析版) 题型:解答题
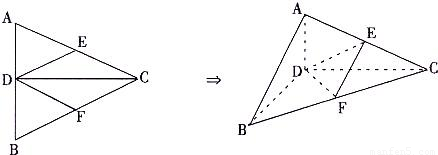
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com