
����Ŀ��ij�����̳�Ϊ���˽�˿͵Ĺ�����Ϣ,������̳��ռ���![]() λ�˿͵Ĺ����ܶ�(��λԪ),�����ݰ���
λ�˿͵Ĺ����ܶ�(��λԪ),�����ݰ���![]()
![]() ��
��![]()
![]() �ֳ�
�ֳ�![]() ��,�Ƴ�������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ:
��,�Ƴ�������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ:
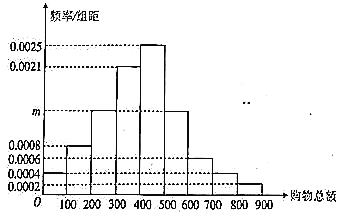
���̳�ÿ�մ�Լ��![]() ���˿�,Ϊ�������̳������ܶ�,���ڶ�һ���Թ��ﲻ����
���˿�,Ϊ�������̳������ܶ�,���ڶ�һ���Թ��ﲻ����![]() Ԫ�Ĺ˿ͷ��ż���Ʒ.
Ԫ�Ĺ˿ͷ��ż���Ʒ.
(1)��Ƶ�ʷֲ�ֱ��ͼ��![]() ��ֵ,������ÿ��Ӧ������Ʒ��������
��ֵ,������ÿ��Ӧ������Ʒ��������
(2)��ÿ�հ��ֲ�����ķ����ӹ����ܶ���![]() �����Ӧ�Ĺ˿��г�ȡ
�����Ӧ�Ĺ˿��г�ȡ![]() ���˿�,��
���˿�,��![]() ���˿����������ȡ���������˿�,ÿ�˽���һ���������,���ó���������������Բ�ͬ��ĸ���.
���˿����������ȡ���������˿�,ÿ�˽���һ���������,���ó���������������Բ�ͬ��ĸ���.
���𰸡���1��![]() ,3650��2��
,3650��2��![]()
��������������(1)����Ƶ�ʷֲ�ֱ��ͼ�У�����С�������֮��Ϊ1�����ʣ��������m��ֵ������Ƶ�ʷֲ�ֱ��ͼ������������ﳬ��300Ԫ�˿͵�Ƶ�ʣ����ݸ��ʼ���������������Ʒ��������
(2) ���ݷֲ������ÿ�����屻���еĸ�����ȣ��ڳ���600Ԫ�Ĺ˿��й���ȡ6��������Ƶ�ʷֲ�ֱ��ͼ�ɵõ����������ֱ�Ϊ3,2,1�������оٷ��оٳ����п��ܣ����ҳ����������Բ�ͬ������������������������Բ�ͬ��ĸ��ʡ�
���: ![]() (1)
(1) ![]()
![]()
![]() ��
��![]()
![]() .
.
���̳�ÿ��Ӧ������Ʒ��������ԼΪ![]()
![]() .
.
(2)��ֱ��ͼ��֪![]() ������������Ϊ
������������Ϊ![]() ,�����������ȡ�������ֱ�Ϊ
,�����������ȡ�������ֱ�Ϊ![]() .
.
����![]() �˷ֱ�Ϊ
�˷ֱ�Ϊ![]() ,
,![]() .���г�ȡ�����
.���г�ȡ�����![]()
![]() ��
��
![]() ��
��![]()
![]() ��15��.
��15��.
�����������Բ�ͬ����![]() ��,���Ի�ó���������������Բ�ͬ��ĸ���Ϊ
��,���Ի�ó���������������Բ�ͬ��ĸ���Ϊ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾������������Ƹ������Ա��ӦƸ�ߴ� T1��T2����������ѡ��һ��μӲ��ԣ��ɼ��ϸ��߿�ǩԼ���ס��ҡ����������˲μ�ӦƸ���ԣ����мס�������ѡ��ʹ������ T1 �� �ұ�ʾֻҪ�ɼ��ϸ��ǩԼ������������ѡ��ʹ������ T2 �� ��Լ�������˳ɼ����ϸ��һͬǩԼ���������˶���ǩԼ����֪�ס��ҿ��Ժϸ�ĸ��ʶ��� ![]() �����������Ժϸ�ĸ��ʶ���
�����������Ժϸ�ĸ��ʶ��� ![]() ���ҿ����Ƿ�ϸ�Ӱ�죮 ��I���������δǩԼ�ĸ��ʣ�
���ҿ����Ƿ�ϸ�Ӱ�죮 ��I���������δǩԼ�ĸ��ʣ�
��II����ǩԼ����Ϊ X���� X�ķֲ��к���ѧ����EX��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��A��B������ֱ�Ϊ����2��0������2��0����ֱ��AP��BP�ཻ�ڵ�P�������ǵ�б��֮���ǩ� ![]() ���ǵ�P�Ĺ켣Ϊ���� �����ķ��̣�
���ǵ�P�Ĺ켣Ϊ���� �����ķ��̣�
������ֱ֪��AP��BP�ֱ�ֱ��l��x=4�ڵ�M��N���켣���ڵ�P�����������߶�MN���ڵ�Q���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ��a��0����a��1����R�ϵ����ݼ����ҹ���x�ķ���|f��x��|=2��xǡ������������ȵ�ʵ���⣬��a��ȡֵ��Χ�ǣ� ��
��a��0����a��1����R�ϵ����ݼ����ҹ���x�ķ���|f��x��|=2��xǡ������������ȵ�ʵ���⣬��a��ȡֵ��Χ�ǣ� ��
A.��0�� ![]() ]
]
B.[ ![]() ��
�� ![]() ]
]
C.[ ![]() ��
�� ![]() ]��{
]��{ ![]() }
}
D.[ ![]() ��
�� ![]() ����{
����{ ![]() }
}
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ,��
,��![]() ҲΪ������
ҲΪ������![]() �Ľ���.(1)��
�Ľ���.(1)��![]() Ϊ��Բ
Ϊ��Բ![]() ������,���߶�
������,���߶�![]() ���е�Ϊ
���е�Ϊ![]() ,��ֱ��
,��ֱ��![]() ��б�ʣ�
��б�ʣ�
(2)������Բ![]() ���ҽ���
���ҽ���![]() ���������ഹֱ��ֱ�߷ֱ���Բ��
���������ഹֱ��ֱ�߷ֱ���Բ��![]() ��
��![]() ,���߶�
,���߶�![]() �ij��ֱ�Ϊ
�ij��ֱ�Ϊ![]() ,֤��
,֤��![]() �Ƕ�ֵ.
�Ƕ�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������6ֻ���ݣ�����2ֻ��Ʒ��4ֻ��Ʒ���зŻصش�����ȡ���Σ�ÿ��ȡһֻ�����������¼��ĸ��ʣ�
��1��ȡ����2ֻ���Ǵ�Ʒ��
��2��ȡ����2ֻ����Ʒ����Ʒ��һֻ��
��3��ȡ����2ֻ��������һֻ��Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=sin��2x+�գ���|��|���У���ͼ������ƽ�� ![]() ����λ�����ԭ��Գƣ�����f��x����[0��
����λ�����ԭ��Գƣ�����f��x����[0�� ![]() ]�ϵ���СֵΪ�� ��
]�ϵ���СֵΪ�� ��
A.�� ![]()
B.�� ![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() ƽ��
ƽ��![]() ���ı���
���ı���![]() ������.
������.
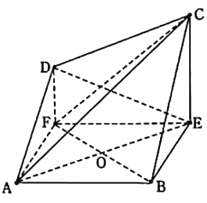
��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��
��![]() ����
����![]() ��������
��������![]() �����.
�����.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com