
【题目】求下列函数的值域和单调区间:
(1)![]() ;
;
(2)![]() .
.
【答案】(1)值域![]() ,增区间
,增区间![]() ,减区间
,减区间![]() ;(2)值域
;(2)值域![]() ,减区间
,减区间![]() ,增区间
,增区间![]() .
.
【解析】
(1)令![]() ,求得
,求得![]() 的取值范围,结合指数函数
的取值范围,结合指数函数![]() 的单调性可求得原函数的值域,利用复合函数的单调性可求得原函数的单调递增区间和递减区间;
的单调性可求得原函数的值域,利用复合函数的单调性可求得原函数的单调递增区间和递减区间;
(2)设![]() ,可得
,可得![]() ,利用二次函数的基本性质可求得原函数的值域,利用复合函数的单调性可得出原函数的单调递增区间和递减区间.
,利用二次函数的基本性质可求得原函数的值域,利用复合函数的单调性可得出原函数的单调递增区间和递减区间.
(1)函数![]() 的定义域为
的定义域为![]() ,设
,设![]() ,则
,则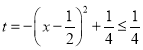 ,
,
又因为指数函数![]() 单调递增,且
单调递增,且![]() ,
,![]() .
.
所以函数![]() 的值域为
的值域为![]() .
.
因为![]() 在区间
在区间![]() 上单调递增,而指数函数
上单调递增,而指数函数![]() 单调递增,
单调递增,
所以,函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
同理,因为![]() 在区间
在区间![]() 上单调递减,而指数函数
上单调递减,而指数函数![]() 单调递增,
单调递增,
所以,函数![]() 的单调递减区间为
的单调递减区间为![]() ;
;
(2)函数![]() 的定义域为
的定义域为![]() ,设
,设![]() ,则
,则![]() .
.
![]() ,
,
所以函数![]() 的值域为
的值域为![]() .
.
因为![]() 在
在![]() 上单调递减,此时由
上单调递减,此时由![]() 得
得![]() .
.
而指数函数![]() 在
在![]() 上单调递增,
上单调递增,
所以,函数![]() 的单调递减区间为
的单调递减区间为![]() .
.
同理,因为![]() 在
在![]() 上单调递增,此时由
上单调递增,此时由![]() 得
得![]() .
.
而指数函数![]() 在
在![]() 上单调递增,
上单调递增,
所以,函数![]() 的单调递增区间为
的单调递增区间为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 为椭圆
为椭圆![]() 的左焦点,离心率为
的左焦点,离心率为![]() ,直线
,直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是弦
是弦![]() 的中点,
的中点,![]() 是椭圆
是椭圆![]() 上一点,求
上一点,求![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始依次按如下规则,将某些整数染成红色,先染1;再染3个偶数2,4,6;再染6后面最邻近的5个连续奇数7,9,11,13,15;再染15后面最邻近的7个连续偶数16,18,20,22,24,26,28;再染此后最邻近的9个连续奇数29,31,![]() ,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,
,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,![]() ,则在这个红色子数列中,由1开始的第1000个数是_________
,则在这个红色子数列中,由1开始的第1000个数是_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com