
已知抛物线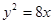 与椭圆
与椭圆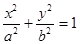 有公共焦点
有公共焦点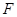 ,且椭圆过点
,且椭圆过点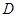
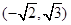 .
.
(1)求椭圆方程;
(2)点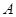 、
、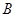 是椭圆的上下顶点,点
是椭圆的上下顶点,点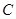 为右顶点,记过点
为右顶点,记过点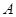 、
、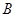 、
、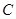 的圆为⊙
的圆为⊙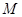 ,过点
,过点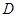 作⊙
作⊙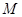 的切线
的切线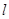 ,求直线
,求直线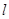 的方程;
的方程;
(3)过椭圆的上顶点作互相垂直的两条直线分别交椭圆于另外一点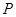 、
、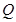 ,试问直线
,试问直线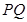 是否经过定点,若是,求出定点坐标;若不是,说明理由.
是否经过定点,若是,求出定点坐标;若不是,说明理由.
(1)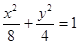 ;(2)
;(2)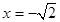 或
或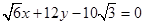 ;(3)
;(3)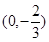 .
.
【解析】
试题分析:(1)由题目给出的条件直接求解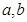 的值,则可求出椭圆方程;(2)当所求直线斜率不存在时,其方程为
的值,则可求出椭圆方程;(2)当所求直线斜率不存在时,其方程为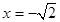 ,符合题意;当直线斜率存在时,可设其斜率为
,符合题意;当直线斜率存在时,可设其斜率为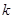 ,写出直线的点斜式方程,因为直线与圆相切,所以根据圆心到直线的距离等于圆的半径可直接求得直线的斜率,从而得到方程;(3)由题意可知,两直线的斜率都存在,设AP:
,写出直线的点斜式方程,因为直线与圆相切,所以根据圆心到直线的距离等于圆的半径可直接求得直线的斜率,从而得到方程;(3)由题意可知,两直线的斜率都存在,设AP: 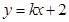 ,代入椭圆的方程从而求出点
,代入椭圆的方程从而求出点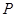 的坐标,同理再求出点
的坐标,同理再求出点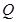 的坐标,从而可求出直线
的坐标,从而可求出直线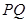 的方程,由方程可知当
的方程,由方程可知当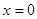 时,
时,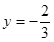 恒成立,所以直线恒过定点
恒成立,所以直线恒过定点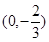 .
.
试题解析:
(1)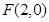 ,则c=2, 又
,则c=2, 又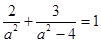 ,得
,得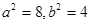
∴所求椭圆方程为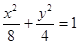 .
.
(2)M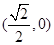 ,⊙M:
,⊙M: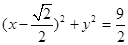 ,直线l斜率不存在时,
,直线l斜率不存在时,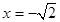 ,
,
直线l斜率存在时,设为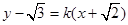 ,
,
∴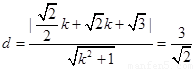 ,解得
,解得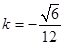 ,
,
∴直线l为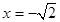 或
或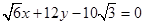 .
.
(3)显然,两直线斜率存在, 设AP: 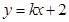 ,
,
代入椭圆方程,得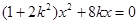 ,解得点
,解得点 ,
,
同理得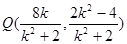 ,直线PQ:
,直线PQ: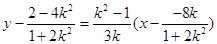 ,
,
令x=0,得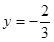 ,∴直线PQ过定点
,∴直线PQ过定点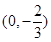 .
.
考点:本题考查了椭圆的标准方程,考查了椭圆的简单几何性质,考查了直线和圆锥曲线的关系,突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.


科目:高中数学 来源:2013-2014学年浙江省高三上学期第三次统练理科数学试卷(解析版) 题型:填空题
已知抛物线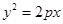 与椭圆
与椭圆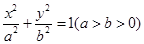 有相同的焦点
有相同的焦点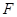 ,
,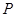 是两曲线的公共点,若
是两曲线的公共点,若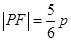 ,则此椭圆的离心率为
.
,则此椭圆的离心率为
.
查看答案和解析>>
科目:高中数学 来源:2010年湖北省高二上学期期中考试数学试卷 题型:解答题
(13分) (理科)已知双曲线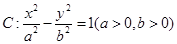 与椭圆
与椭圆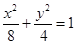 有公共焦点,且以抛物线
有公共焦点,且以抛物线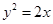 的准线为双曲线
的准线为双曲线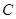 的一条准线.动直线
的一条准线.动直线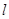 过双曲线
过双曲线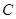 的右焦点
的右焦点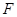 且与双曲线的右支交于
且与双曲线的右支交于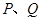 两点.
两点.
(1)求双曲线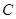 的方程;
的方程;
(2)无论直线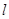 绕点
绕点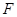 怎样转动,在双曲线
怎样转动,在双曲线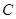 上是否总存在定点
上是否总存在定点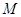 ,使
,使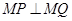 恒成立?若存在,求出点
恒成立?若存在,求出点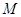 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线![]() 与椭圆
与椭圆![]() 有公共焦点,且以抛物线
有公共焦点,且以抛物线![]() 的准线为双曲线
的准线为双曲线![]() 的一条准线.动直线
的一条准线.动直线![]() 过双曲线
过双曲线![]() 的右焦点
的右焦点![]() 且与双曲线的右支交于
且与双曲线的右支交于![]() 两点.
两点.
(1)求双曲线![]() 的方程;
的方程;
(2)无论直线![]() 绕点
绕点![]() 怎样转动,在双曲线
怎样转动,在双曲线![]() 上是否总存在定点
上是否总存在定点![]() ,使
,使![]() 恒成立?若存在,求出点
恒成立?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011年重庆十一中高考数学一模训练试卷(二)(解析版) 题型:解答题
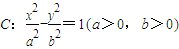 与椭圆
与椭圆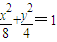 有公共焦点,且以抛物线y2=2x的准线为双曲线C的一条准线.动直线l过双曲线C的右焦点F且与双曲线的右支交于P、Q两点.
有公共焦点,且以抛物线y2=2x的准线为双曲线C的一条准线.动直线l过双曲线C的右焦点F且与双曲线的右支交于P、Q两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com