


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练8练习卷(解析版) 题型:选择题
知函数y=f(x)的值域为C,若函数x=g(t)使函数y=f[g(t)]的值域仍为C,则称x=g(t)是y=f(x)的一个等值域变换,下列函数中,x=g(t)是y=f(x)的一个等值域变换的为( )
(A)f(x)=2x+b,x∈R,x=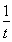
(B)f(x)=ex,x∈R,x=cost
(C)f(x)=x2,x∈R,x=et
(D)f(x)=|x|,x∈R,x=lnt
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海外国语大学附中高三(上)第一次周练数学试卷(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年绵阳市诊断三文) 已知y=f(x)是其定义域上的单调递增函数,它的反函数是y=f--1(x),且y=f(x+1)的图象过A(-4,0),B(2,3)两点,若![]() ,则x的取值范围是
,则x的取值范围是
A.[0,3] B.[-4,2] C.[-1,2] D.[1,3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com