
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.

(1)若![]() 点是
点是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 成角的正弦值.
成角的正弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知若![]() ,则称
,则称![]() 为
为![]() 的原函数,此时
的原函数,此时![]() 所有的原函数为
所有的原函数为![]() ,其中
,其中![]() 为常数,如:
为常数,如:![]() ,则
,则![]() (
(![]() 为常数).现已知函数
为常数).现已知函数![]() 的导函数为
的导函数为![]() 且对任意的实数
且对任意的实数![]() 都有
都有![]() (
(![]() 是自然对数的底数),且
是自然对数的底数),且![]() ,若关于
,若关于![]() 的不等式
的不等式![]() 的解集中恰有两个整数,则实数
的解集中恰有两个整数,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过去大多数人采用储蓄的方式将钱储蓄起来,以保证自己生活的稳定,考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式,随着金融业的发展,普通人能够使用的投资理财工具也多了起来,为了研究某种理财工具的使用情况,现对![]() 年龄段的人员进行了调查研究,将各年龄段人数分成
年龄段的人员进行了调查研究,将各年龄段人数分成![]() 组:
组:![]() ,并整理得到频率分布直方图:
,并整理得到频率分布直方图:
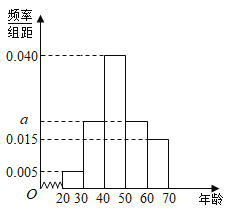
(1)求图中的![]() 值;
值;
(2)采用分层抽样的方法,从第二组、第三组、第四组中共抽取![]() 人,则三个组中各抽取多少人?
人,则三个组中各抽取多少人?
(3)在(2)中抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,则这
人,则这![]() 人都来自于第三组的概率是多少?
人都来自于第三组的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日上午,山东省省委、省政府在济南召开山东省全面展开新旧动能转换重大工程动员大会,会议动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了200件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.图3是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
内的产品视为合格品,否则为不合格品.图3是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
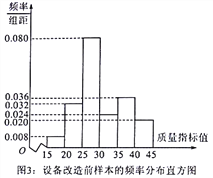
表1:设备改造后样本的频数分布表

(1)完成下面的![]() 列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;

(2)根据图3和表1提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)企业将不合格品全部销毁后,根据客户需求对合格品进行等级细分,质量指标值落在![]() 内的定为一等品,每件售价240元;质量指标值落在
内的定为一等品,每件售价240元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件售价180元;其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
内的定为二等品,每件售价180元;其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
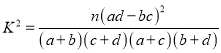
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() 存在单调增区间,求
存在单调增区间,求![]() 的取值范围;
的取值范围;
(Ⅱ)是否存在实数![]() ,使得方程
,使得方程![]() 在区间
在区间![]() 内有且只有两个不相等的实数根?若存在,求出
内有且只有两个不相等的实数根?若存在,求出![]() 的取值范围?若不存在,请说明理由.
的取值范围?若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,
,![]() ,
,![]() 分别是椭圆短轴的上下两个端点,
分别是椭圆短轴的上下两个端点,![]() 是椭圆的左焦点,P是椭圆上异于点
是椭圆的左焦点,P是椭圆上异于点![]() ,
,![]() 的点,若
的点,若![]() 的边长为4的等边三角形.
的边长为4的等边三角形.
![]() 写出椭圆的标准方程;
写出椭圆的标准方程;
![]() 当直线
当直线![]() 的一个方向向量是
的一个方向向量是![]() 时,求以
时,求以![]() 为直径的圆的标准方程;
为直径的圆的标准方程;
![]() 设点R满足:
设点R满足:![]() ,
,![]() ,求证:
,求证:![]() 与
与![]() 的面积之比为定值.
的面积之比为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com