
| 3 |
| 3 |
|
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
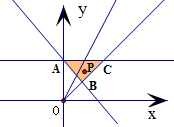 解:(I)∵P点的坐标为(-
解:(I)∵P点的坐标为(-| 3 |
| 3+1 |
| 1 |
| 2 |
-
| ||
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 7π |
| 12 |
| 5π |
| 6 |
| π |
| 4 |
| 7π |
| 12 |
| ||||
| 2 |
| π |
| 2 |
| 5π |
| 6 |
| ||||
| 2 |
| 3 |


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
| a |
| 2 |
| b |
| π |
| 4 |
| a |
| b |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (考生注意:只能从下列A、B、C三题中选做一题,如果多做,则按第一题评阅记分)
(考生注意:只能从下列A、B、C三题中选做一题,如果多做,则按第一题评阅记分)
|
| |x+1|+|x-2|-a |
| 5 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练17练习卷(解析版) 题型:解答题
设函数f(θ)= sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
(1)若点P的坐标为( ,
, ),求f(θ)的值;
),求f(θ)的值;
(2)若点P(x,y)为平面区域Ω:  上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
查看答案和解析>>
科目:高中数学 来源:福建省高考真题 题型:解答题
 sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π,
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π,  ,求f(θ)的值;
,求f(θ)的值;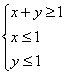 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com