
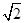 ,E为PD上一点,PE = 2ED.
,E为PD上一点,PE = 2ED.
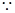 PA =" PD" =" 1" ,PD =" 2" ,
PA =" PD" =" 1" ,PD =" 2" , 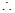 PA2 + AD2 = PD2, 即:PA ^ AD---2分
PA2 + AD2 = PD2, 即:PA ^ AD---2分
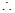 PA ^平面ABCD-------4分
PA ^平面ABCD-------4分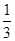 ,PA =
,PA = 
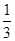 , ------5分
, ------5分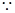 GH ^ AC ,
GH ^ AC , 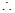 EH ^ AC ,
EH ^ AC ,  Ð EHG为二面角D—AC―E的平面角.-----6分
Ð EHG为二面角D—AC―E的平面角.-----6分 tanÐEHG =
tanÐEHG =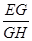 =
= 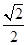 . -------8分
. -------8分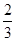 ,
,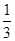 ),
),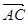 =" (1,1,0),"
=" (1,1,0)," 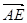 =" (0" ,
=" (0" , 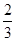 ,
,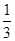 )---9分
)---9分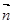 =" (x," y,z) , 则
=" (x," y,z) , 则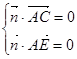 ,即:
,即: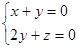 , 令y =" 1" ,
, 令y =" 1" , 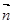 =" (-" 1,1, - 2 )-------------10分
=" (-" 1,1, - 2 )-------------10分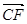 =
= 
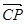 ,
,  £ 1), 使得:BF//平面AEC, 则
£ 1), 使得:BF//平面AEC, 则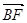 ×
×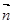 = 0. 又因为:
= 0. 又因为: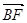 =
= 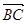 +
+ 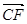 = (0 ,1,0)+
= (0 ,1,0)+  ,-
,- ,
, )= (-
)= (- ,1-
,1- ,
, ),
),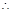
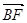 ×
×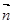 =
= + 1-
+ 1-  - 2
- 2 =" 0" ,
=" 0" , 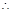
 = ,所以存在PD的中点F,
= ,所以存在PD的中点F, 

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源:不详 题型:解答题
 平面ABD,AE=a。
平面ABD,AE=a。 ,求证:AB//平面CDE;
,求证:AB//平面CDE;

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
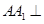 平面
平面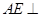 平面A1BD;
平面A1BD;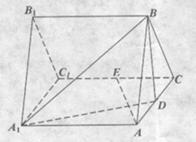
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com