练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为0.08，只选修甲和乙的概率是0.12，至少选修一门的概率是0.88，用表示该学生选修的课程门数和没有选修的课程门数的乘积.

       记“函数为R上的偶函数”为事件A，求事件A的概率；

     

    【答案】

    设该学生选修甲、乙、丙的概率分别为x、y、z

           依题意得            

    （I）                    若函数为R上的偶函数，则=0     

           当=0时，表示该学生选修三门功课或三门功课都没选.

          

           =0.4×0.5×0.6+（1－0.4）（1－0.5）（1－0.6）=0.24

           ∴事件A的概率为0.24 

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响．已知某学生选修甲而不选修乙和丙的概率为0.08，选修甲和乙而不选修丙的概率是0.12，至少选修一门的概率是0.88，用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积．
    （1）记“函数f（x）=x2+ξ•x为R上的偶函数”为事件A，求事件A的概率；
    （2）求ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响．已知学生小张只选甲的概率为0.08，只选修甲和乙的概率是0.12，至少选修一门的概率是0.88，用ξ表示小张选修的课程门数和没有选修的课程门数的乘积．
    （Ⅰ）求学生小张选修甲的概率；
    （Ⅱ）记“函数f（x）=x2+ξx为R上的偶函数”为事件A，求事件A的概率；
    （Ⅲ）求ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响.已知某学生选修甲而不选修乙和丙的概率为0.08，选修甲和乙而不选修丙的概率是0.12，至少选修一门课的概率是0.88，用表示该学生选修的课程门数和没有  选修的课程门数的乘积.

    （1）记“函数f（x）=x2+·x为R上的偶函数”为事件A，求事件A的概率；

    （2）求的概率分布和数学期望.

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年广东省等三校高三2月月考数学理卷 题型：解答题

    （本小题满分14分）

    某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响. 已知学生小张只选甲的概率为，只选修甲和乙的概率是，至少选修一门的概率是，用表示小张选修的课程门数和没有选修的课程门数的乘积.

       （Ⅰ）求学生小张选修甲的概率；

    （Ⅱ）记“函数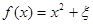 为上的偶函数”为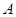事件，求事件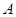的概率；

                    （Ⅲ）求的分布列和数学期望。                                    

          

    查看答案和解析>>

    同步练习册答案