
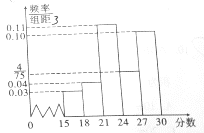
【题目】某中学为调查高三学生英语听力水平的情况,随机抽取了高三年级的80名学生进行测试,根据测试结果绘制了英语听力成绩(满分为30分)的频率分布直方图,将成绩不低于27分的定为优秀
(1)根据已知条件完成下面的![]() 列联表,并据此资料判断是否有90%的把握认为英语听力成绩是否优秀与性别有关?
列联表,并据此资料判断是否有90%的把握认为英语听力成绩是否优秀与性别有关?
英语听力优秀 | 非英语听力优秀 | 合计 | |
男同学 | 10 | ||
女同学 | 36 | ||
合计 |
(2)将上述调查所得到的频率视为概率,现在从该校高三学生中,采取随机抽样方法每次抽取1名学生,共抽取3次,记被抽取的3名学生中“英语听力优秀”的人数为X,若每次抽取的结果是相互独立的,求X的分布列和数学期望E(X)
参考公式: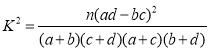 ,其中
,其中![]()
参考临界值:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)联表见详解,没有90%的把握认为“英语听力优秀”与性别有关(2)分布列详见解析,期望0.9.
【解析】
(1)根据题目所给的数据填写![]() 列联表即可;再计算
列联表即可;再计算![]() 的观测值
的观测值![]() ,对照题目中的表格,得出统计结论;(2)将频率视为概率,得到学生中抽到一名“英语听力优秀”的概率,根据二项分布即可求解.
,对照题目中的表格,得出统计结论;(2)将频率视为概率,得到学生中抽到一名“英语听力优秀”的概率,根据二项分布即可求解.
(1)由频率分布直方图可知,在80人中, “英语听力优秀”有24人,从而2x 2列联表如下:
英语听力优秀 | 非英语听力优秀 | 合计 | |
男同学 | 10 | 34 | 44 |
女同学 | 14 | 22 | 36 |
合计 | 24 | 56 | 80 |
将![]() 列联表中的数据代入公式计算,得:
列联表中的数据代入公式计算,得:
![]() ,
,
因为2.463 < 2.706,所以没有90%的把握认为“英语听力优秀”与性别有关.
(2)由频率分布直方图知抽到“英语听力优秀”的频率为0.3,将频率视为概率,即从学
生中抽取一名“英语听力优秀”的概率为0.3,由题意![]() ,
,
从而X的分布列为:

![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(2)是否存在实数![]() ,使得对任意
,使得对任意![]() ,存在
,存在![]() ,不等式
,不等式![]() 成立?若存在,求出
成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】越接近高考学生焦虑程度越强,四个高三学生中大约有一个有焦虑症,经有关机构调查,得出距离高考周数与焦虑程度对应的正常值变化情况如下表周数
周数x | 6 | 5 | 4 | 3 | 2 | 1. |
正常值y | 55 | 63 | 72 | 80 | 90 | 99 |
其中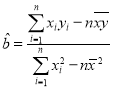 ,
,![]() ,
,![]() ,
,![]()
(1)作出散点图;
(2)根据上表数据用最小二乘法求出y关于x的线性回方程![]() (精确到0.01)
(精确到0.01)
(3)根据经验观测值为正常值的0.85~1.06为正常,若1.06~1.12为轻度焦虑,1.12~1.20为中度焦虑,1.20及以上为重度焦虑。若为中度焦虑及以上,则要进行心理疏导。若一个学生在距高考第二周时观测值为103,则该学生是否需要进行心理疏导?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知直线l1的参数方程为![]() (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为 (t为参数),其中α∈(0,
(t为参数),其中α∈(0,![]() ),以原点O为点x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,曲线C的极坐标方程为ρ﹣2sinθ=0.
),以原点O为点x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,曲线C的极坐标方程为ρ﹣2sinθ=0.
(1)写出直线l1的极坐标方程和曲线C的直角坐标方程;
(2)设直线l1,l2分别与曲线C交于点A,B(非坐标原点)求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,例如求1到2000这2000个整数中,能被3除余1且被7除余1的数的个数,现由程序框图,其中MOD函数是一个求余函数,记![]() 表示m除以n的余数,例如
表示m除以n的余数,例如![]() ,则输出i为( ).
,则输出i为( ).
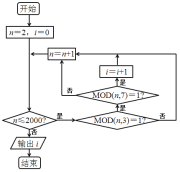
A.98B.97C.96D.95
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (α为参数).以坐标原点O为极点,x轴正半轴为极轴的坐标系中,曲线C2的方程为
(α为参数).以坐标原点O为极点,x轴正半轴为极轴的坐标系中,曲线C2的方程为![]() (m为常数)
(m为常数)
(1)求曲线C1,C2的直角坐标方程;
(2)若曲线C1,C2有两个交点P、Q,当|PQ|![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着银行业的不断发展,市场竞争越来越激烈,顾客对银行服务质量的要求越来越高,银行为了提高柜员,员工的服务意识,加强评价管理,工作中让顾客对服务作出评价,评价分为满意、基本满意、不满意三种,某银行为了比较顾客对男女柜员员工满意度评价的差异,在下属的四个分行中随机抽出40人(男女各半)进行分析比较对40人一月中的顾客评价“不满意“的次数进行了统计,按男、女分为两组,再将每组柜员员工的月“不满意”次数分为5组:[0,5),[5,10),[10,15),[15,20),[20,25],得到如下频数分布表.
分组 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25] |
女柜员 | 2 | 3 | 8 | 5 | 2 |
男柜员 | 1 | 3 | 9 | 4 | 3 |
(1)在答题卡所给的坐标系中分别画出男、女柜员员工的频率分布直方图;并求出男、女柜员的月平均“不满意”次数的估计值,试根据估计值比较男、女柜员的满意度谁高?
(2)在抽取的40名柜员员工中,从“不满意”次数不少于20的柜员员工中随机抽取3人,求抽取的3人中,男柜员不少于女柜员的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com