
【题目】数学家欧拉在![]() 年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线后人称之为三角形的欧拉线.已知
年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线后人称之为三角形的欧拉线.已知![]() 的顶点
的顶点![]() 、
、![]() ,若其欧拉线方程为
,若其欧拉线方程为![]() ,则顶点
,则顶点![]() 的坐标是( )
的坐标是( )
参考公式:若![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 的坐标分别是
的坐标分别是![]() 、
、![]() 、
、![]() ,则该
,则该![]() 的重心的坐标为
的重心的坐标为![]() .
.
A.![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]()
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】攀枝花是一座资源富集的城市,矿产资源储量巨大,已发现矿种76种,探明储量39种,其中钒、钛资源储量分别占全国的63%和93%,占全球的11%和35%,因此其素有“钒钛之都”的美称.攀枝花市某科研单位在研发钛合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值y(y值越大产品的性能越好)与这种新合金材料的含量x(单位:克)的关系为:当0≤x<7时,y是x的二次函数;当x≥7时,![]() .测得部分数据如表:
.测得部分数据如表:

(1)求y关于x的函数关系式y=f(x);
(2)求该新合金材料的含量x为何值时产品的性能达到最佳.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高二年级学生中随机抽取100名学生,将他们某次考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示),
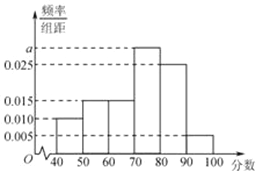
(1)求分数在[70,80)中的人数;
(2)若用分层抽样的方法从分数在[40,50)和[50,60)的学生中共抽取5 人,该5 人中成绩在[40,50)的有几人?
(3)在(2)中抽取的5人中,随机选取2 人,求分数在[40,50)和[50,60)各1 人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实数a,b满足ab>0且a≠b,由a、b、![]() 、
、![]() 按一定顺序构成的数列( )
按一定顺序构成的数列( )
A. 可能是等差数列,也可能是等比数列
B. 可能是等差数列,但不可能是等比数列
C. 不可能是等差数列,但可能是等比数列
D. 不可能是等差数列,也不可能是等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() ,且焦点为F,直线l与抛物线相交于A,B两点.
,且焦点为F,直线l与抛物线相交于A,B两点.
⑴求抛物线C的方程,并求其准线方程;
⑵![]() 为坐标原点.若
为坐标原点.若![]() ,证明直线l必过一定点,并求出该定点.
,证明直线l必过一定点,并求出该定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com