
【题目】已知定义在[0,+∞)上的函数f(x)满足f(x)=2f(x+2),当x∈[0,2)时,f(x)=﹣2x2+4x.设f(x)在[2n﹣2,2n)上的最大值为an(n∈N*),且{an}的前n项和为Sn , 则Sn=( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:∵定义在[0,+∞)上的函数f(x)满足f(x)=2f(x+2), ∴f(x+2)= ![]() f(x),
f(x),
∴f(x+4)= ![]() f(x+2)=
f(x+2)= ![]() f(x),f(x+6)=
f(x),f(x+6)= ![]() f(x+4)=
f(x+4)= ![]() f(x),…f(x+2n)=
f(x),…f(x+2n)= ![]() f(x)
f(x)
设x∈[2n﹣2,2n),则x﹣(2n﹣2)∈[0,2)
∵当x∈[0,2)时,f(x)=﹣2x2+4x.
∴f[x﹣(2n﹣2)]=﹣2[(x﹣(2n﹣2)]2+4[x﹣(2n﹣2)].
∴ ![]() =﹣2(x﹣2n+1)2+2
=﹣2(x﹣2n+1)2+2
∴f(x)=21﹣n[﹣2(x﹣2n+1)2+2],x∈[2n﹣2,2n),
∴x=2n﹣1时,f(x)的最大值为22﹣n
∴an=22﹣n
∴{an}表示以2为首项, ![]() 为公比的等比数列
为公比的等比数列
∴{an}的前n项和为Sn=  =
= ![]()
故选B.


科目:高中数学 来源: 题型:
【题目】已知某校5个学生期末考试数学成绩和总分年级排名如下表:
学生的编号 | 1 | 2 | 3 | 4 | 5 |
数学 | 115 | 112 | 93 | 125 | 145 |
年级排名 | 250 | 300 | 450 | 70 | 10 |
(1)通过大量事实证明发现,一个学生的数学成绩和总分年级排名具有很强的线性相关关系,在上述表格是正确的前提下,用![]() 表示数学成绩,用
表示数学成绩,用![]() 表示年级排名,求
表示年级排名,求![]() 与
与![]() 的回归方程;(其中
的回归方程;(其中![]() 都取整数)
都取整数)
(2)若在本次考试中,预计数学分数为120分的学生年级排名大概是多少?
参考数据和公式:![]() ,其中
,其中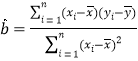 ,
,![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}中,其前n项和为Sn , 且 ![]() ,等比数列{bn}中,其前n项和为Tn , 且
,等比数列{bn}中,其前n项和为Tn , 且 ![]() ,(n∈N*)
,(n∈N*)
(1)求an , bn;
(2)求{anbn}的前n项和Mn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|. (Ⅰ)若不等式f(x)≤2的解集为[0,4],求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若x0∈R,使得f(x0)+f(x0+5)﹣m2<4m,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线l的参数方程为 ![]() (t为参数,0<α<π),曲线C的极坐标方程为ρsin2θ=4cosθ. (Ⅰ)求曲线C的直角坐标方程;
(t为参数,0<α<π),曲线C的极坐标方程为ρsin2θ=4cosθ. (Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)设直线l与曲线C相交于A、B两点,当α变化时,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,AC=BC=5,AB=6,M是CC1中点,CC1=8. 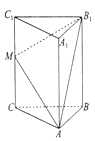
(1)求证:平面AB1M⊥平面A1ABB1;
(2)求平面AB1M与平面ABC所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣
x3﹣ ![]() x2+logax,(a>0且a≠1)为定义域上的增函数,f'(x)是函数f(x)的导数,且f'(x)的最小值小于等于0. (Ⅰ)求a的值;
x2+logax,(a>0且a≠1)为定义域上的增函数,f'(x)是函数f(x)的导数,且f'(x)的最小值小于等于0. (Ⅰ)求a的值;
(Ⅱ)设函数 ![]() ,且g(x1)+g(x2)=0,求证:
,且g(x1)+g(x2)=0,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com