
科目:高中数学 来源: 题型:
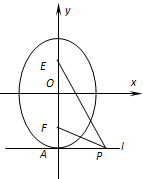 (1)已知平面上两定点A(-2,0).B(2,0),且动点M标满足
(1)已知平面上两定点A(-2,0).B(2,0),且动点M标满足| MA |
| MB |
| y2 |
| 25 |
| x2 |
| 16 |
| y2 |
| 25 |
| x2 |
| 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2007•金山区一模)(1)已知平面上两定点A(-2,0)、B(2,0),且动点M的坐标满足
(2007•金山区一模)(1)已知平面上两定点A(-2,0)、B(2,0),且动点M的坐标满足| MA |
| MB |
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| b |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本大题18分)
(1)已知平面上两定点![]() .
.![]() ,且动点M标满足
,且动点M标满足![]() =0,求动点
=0,求动点![]() 的轨迹方程;
的轨迹方程;
(2)若把(1)的M的轨迹图像向右平移一个单位,再向下平移一个单位,恰与直线x+ky–3=0 相切,试求实数k的值;
(3)如图,l是经过椭圆![]() 长轴顶点A且与长轴垂直的直线,E.F是两个焦点,点PÎl,P不与A重合。若ÐEPF=
长轴顶点A且与长轴垂直的直线,E.F是两个焦点,点PÎl,P不与A重合。若ÐEPF=![]() ,求
,求![]() 的取值范围。
的取值范围。
并将此题类比到双曲线:![]() ,
,![]() 是经过焦点
是经过焦点![]() 且与实轴垂直的直线,
且与实轴垂直的直线,![]() 是两个顶点,点PÎl,P不与
是两个顶点,点PÎl,P不与![]() 重合,请作出其图像。若
重合,请作出其图像。若![]() ,写出角
,写出角![]() 的取值范围。(不需要解题过程)
的取值范围。(不需要解题过程)

查看答案和解析>>
科目:高中数学 来源: 题型:
|
下列命题中不正确命题的个数是 ( ) ①经过空间一点一定可作一平面与两异面直线都平行; ②已知平面、,直线a、b,若,,则; ③有两个侧面垂直于底面的四棱柱为直四棱柱; ④四个侧面两两全等的四棱柱为直四棱柱; ⑤底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥; ⑥底面是等边三角形,∠APB=∠BPC=∠CPA,则三棱锥P-ABC是正三棱锥. A.0 B.1 C.2 D.3 查看答案和解析>> 科目:高中数学 来源: 题型: 吉林省吉林一中2011届高三下学期冲刺试题一(数学理).doc | | |
|