
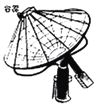
【题目】如图是一种加热食物的太阳灶,上面装有可旋转的抛物面形的反光镜,镜的轴截面是抛物线的一部分,盛食物的容器放在抛物线的焦点处,容器由若干根等长的铁筋焊接在一起的架子支撑.已知镜口圆的直径为8m,镜深1m.
(1)建立适当的坐标系,求抛物线的方程和焦点的位置;
(2)若把盛水和食物的容器近似地看作点,试求每根铁筋的长度.
【答案】(1)标准方程是y2=16x,焦点坐标是F(4,0)(2)5
【解析】
(1)在反光镜的轴截面内建立平面直角坐标系,使反光镜的顶点(即抛物线的顶点)与原点重合,x轴垂直于镜口直径,根据点A(1,4)可以求出抛物线的标准方程;(2)由题得A、F两点间的距离即为每根铁筋长,求|AF|的长度即可得解.
解:(1)在反光镜的轴截面内建立平面直角坐标系,如图所示;
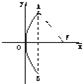
使反光镜的顶点(即抛物线的顶点)与原点重合,x轴垂直于镜口直径;
由已知,得A点坐标是(1,4),
设抛物线方程为y2=2px(p>0),
则16=2p×1,求得p=8;
所以所求抛物线的标准方程是y2=16x,
所以焦点坐标是F(4,0).
(2)盛水的容器在焦点处,所以A、F两点间的距离即为每根铁筋长.
计算|AF|=x1+![]() =1+4=5,即每根铁筋的长度是5m.
=1+4=5,即每根铁筋的长度是5m.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,
, ![]() ).
).
(1)当![]() 时,若
时,若![]() 在其定义域内为单调函数,求
在其定义域内为单调函数,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立,如果存在,求
恒成立,如果存在,求![]() 的取值范围,如果不存在,说明理由.
的取值范围,如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为![]() nmile/h,在甲船从A岛出发的同时,乙船从A岛正南
nmile/h,在甲船从A岛出发的同时,乙船从A岛正南![]() nmile处的B岛出发,朝北偏东30°的方向作匀速直线航行,速度为
nmile处的B岛出发,朝北偏东30°的方向作匀速直线航行,速度为![]() nmile/h.
nmile/h.

(1)若两船能相遇,求m;
(2)当![]() 时,两船出发2小时后,求两船之间的距离.
时,两船出发2小时后,求两船之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1:![]() +
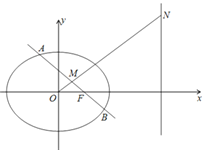
+![]() =1(a>b>0)的右焦点F(1,0),右准线l:x=4.圆C2:x2+y2=b2.A、B为椭圆上不同的两点,AB中点为M.
=1(a>b>0)的右焦点F(1,0),右准线l:x=4.圆C2:x2+y2=b2.A、B为椭圆上不同的两点,AB中点为M.
(1)求椭圆C1的方程;
(2)若直线AB过F点,直线OM交l于N点,求证:NF⊥AB;
(3)若直线AB与圆C2相切,求原点O到AB中垂线的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:已知四棱锥P—ABCD的底面ABCD是平行四边形,PA⊥面ABCD,M是AD的中点,N是PC的中点.

(1)求证:MN∥面PAB;
(2)若平面PMC⊥面PAD,求证:CM⊥AD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com