
【题目】设数列{an}的前n项和为Sn . 已知a1=1, ![]() =an+1﹣
=an+1﹣ ![]() n2﹣n﹣
n2﹣n﹣ ![]() ,n∈N* .
,n∈N* .
(1)求数列{an}的通项公式;
(2)设数列{bn}满足an﹣an﹣1=bna ![]() ,求数列{bn}的n前项和Tn;
,求数列{bn}的n前项和Tn;
(3)是否存在实数λ,使得不等式λa ![]() ﹣
﹣ ![]() +a
+a ![]() +
+ ![]() ≥0恒成立,若存在,求出λ的取值范围;若不存在,请说明理由.
≥0恒成立,若存在,求出λ的取值范围;若不存在,请说明理由.
【答案】
(1)解:∵ ![]() ,n∈N*.
,n∈N*.
∴ ![]() ①
①
∴当n≥2时, ![]() ②
②
由①﹣②,得
2Sn﹣2Sn﹣1=nan+1﹣(n﹣1)an﹣n(n+1).
∵2an=2Sn﹣2Sn﹣1
∴2an=nan+1﹣(n﹣1)an﹣n(n+1),
∴ ![]() ,
,
∴数列 ![]() 是以首项为
是以首项为 ![]() ,公差为1的等差数列.
,公差为1的等差数列.
∴ ![]() ,
,
∴ ![]() ,当n=1时,上式显然成立.
,当n=1时,上式显然成立.
∴ ![]()
(2)an﹣an﹣1=bna ![]() bn=
bn= ![]() =
= ![]() =
= ![]() .
.
∴Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .①
.①
![]() Tn=
Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .②
.②
由①﹣②,得
![]() Tn=
Tn= ![]() +2(
+2( ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() )﹣
)﹣ ![]() .
.
= ![]() +2
+2 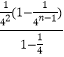 ﹣
﹣ ![]() .
.
∴Tn= ![]() ﹣
﹣ ![]() ,n∈N+
,n∈N+
(3)λa ![]() ﹣
﹣ ![]() +a
+a ![]() +
+ ![]() ≥0λ(2n﹣
≥0λ(2n﹣ ![]() )+2n+
)+2n+ ![]() ≥0,(n=2,4,6,8,10…)λ(2n﹣
≥0,(n=2,4,6,8,10…)λ(2n﹣ ![]() )+(2n﹣
)+(2n﹣ ![]() )2+2≥0,
)2+2≥0,
令t=2n﹣ ![]() ,则t≥
,则t≥ ![]() ,
,
原不等式λt+t2+2≤0≥﹣(t+ ![]() ).
).
∵t+ ![]() 在(
在( ![]() ,+∞)上单调递增,
,+∞)上单调递增,
∴t+ ![]() ≥
≥ ![]() +
+ ![]() .
.
∴λ≥﹣ ![]()
【解析】(1)需要分类讨论:n=1和n≥2两种情况下的通项公式.当n≥2时,根据已知条件可以推知2Sn﹣2Sn﹣1=nan+1﹣(n﹣1)an﹣n(n+1).2an=nan+1﹣(n﹣1)an﹣n(n+1),由着两个式子可以得到数列 ![]() 是以首项为
是以首项为 ![]() ,公差为1的等差数列.由此写出通项公式即可;(2)由an﹣an﹣1=bna
,公差为1的等差数列.由此写出通项公式即可;(2)由an﹣an﹣1=bna ![]() 可得bn=
可得bn= ![]() =
= ![]() =
= ![]() .再利用“错位相减法”与等比数列的求和公式即可得出;(3)将已知不等式变形为λ(2n﹣
.再利用“错位相减法”与等比数列的求和公式即可得出;(3)将已知不等式变形为λ(2n﹣ ![]() )+(2n﹣
)+(2n﹣ ![]() )2+2≥0,然后结合函数的单调性来求λ的取值范围.
)2+2≥0,然后结合函数的单调性来求λ的取值范围.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系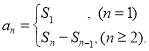 .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F. 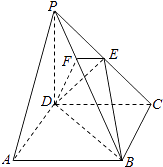
(1)证明PA∥平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C﹣PB﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px过点P(1,1).过点(0,![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.
(Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A为线段BM的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“一带一路”的建设中,中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了几口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料下表:
井号I | 1 | 2 | 3 | 4 | 5 | 6 |
坐标 |
|
|
|
|
|
|
钻探深度 | 2 | 4 | 5 | 6 | 8 | 10 |
出油量 | 40 | 70 | 110 | 90 | 160 | 205 |
(1)在散点图中![]() 号旧井位置大致分布在一条直线附近,借助前5组数据求得回归线方程为
号旧井位置大致分布在一条直线附近,借助前5组数据求得回归线方程为![]() ,求
,求![]() ,并估计
,并估计![]() 的预报值;
的预报值;
(2)现准备勘探新井![]() ,若通过1、3、5、7号井计算出的
,若通过1、3、5、7号井计算出的![]() 的值(
的值(![]() 精确到0.01)相比于(1)中
精确到0.01)相比于(1)中![]() 的值之差(即:
的值之差(即: ![]() )不超过10%,则使用位置最接近的已有旧井
)不超过10%,则使用位置最接近的已有旧井![]() ,否则在新位置打井,请判断可否使用旧井?(参考公式和计算结果:
,否则在新位置打井,请判断可否使用旧井?(参考公式和计算结果: 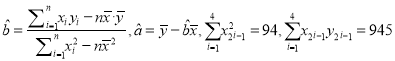 )
)
(3)设出油量与钻探深度的比值![]() 不低于20的勘探井称为优质井,在原有井号
不低于20的勘探井称为优质井,在原有井号![]() 的井中任意勘探3口井,求恰好2口是优质井的概率.
的井中任意勘探3口井,求恰好2口是优质井的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C的对边分别为a,b,c,且a>c,已知 ![]()
![]() =2,cosB=
=2,cosB= ![]() ,b=3,求:
,b=3,求:
(Ⅰ)a和c的值;
(Ⅱ)cos(B﹣C)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 过点
过点 ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,且
,且![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的上顶点,过点
的上顶点,过点![]() 分别作直线
分别作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为![]() ,且
,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,
, ![]() 满足|
满足| ![]() |=
|= ![]() ,|
,| ![]() |=1,且对任意实数x,不等式|
|=1,且对任意实数x,不等式| ![]() +x
+x ![]() |≥|
|≥| ![]() +
+ ![]() |恒成立,设
|恒成立,设 ![]() 与
与 ![]() 的夹角为θ,则tan2θ=( )
的夹角为θ,则tan2θ=( )
A.﹣ ![]()
B.![]()
C.﹣ ![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com