
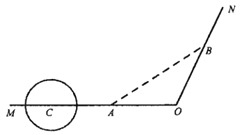
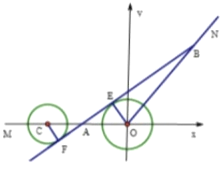
【题目】为解决城市的拥堵问题,某城市准备对现有的一条穿城公路MON进行分流,已知穿城公路MON自西向东到达城市中心![]() 后转向
后转向![]() 方向,已知∠MON=
方向,已知∠MON=![]() ,现准备修建一条城市高架道路L,L在MO上设一出入口A,在ON上设一出口B,假设高架道路L在AB部分为直线段,且要求市中心
,现准备修建一条城市高架道路L,L在MO上设一出入口A,在ON上设一出口B,假设高架道路L在AB部分为直线段,且要求市中心![]() 与AB的距离为10km.
与AB的距离为10km.
(1)求两站点A,B之间的距离;
(2)公路MO段上距离市中心![]() 30km处有一古建筑群C,为保护古建筑群,设立一个以C为圆心,5km为半径的圆形保护区.因考虑未来道路AB的扩建,则如何在古建筑群和市中心
30km处有一古建筑群C,为保护古建筑群,设立一个以C为圆心,5km为半径的圆形保护区.因考虑未来道路AB的扩建,则如何在古建筑群和市中心![]() 之间设计出入口A,才能使高架道路及其延伸段不经过保护区?
之间设计出入口A,才能使高架道路及其延伸段不经过保护区?
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)过O作直线OE⊥AB于E,则OE=10,设∠EOA=![]() ,可求∠EOB=
,可求∠EOB=![]() ﹣
﹣![]() ,(
,(![]() ),可得AE=10tan
),可得AE=10tan![]() ,BE=10tan(
,BE=10tan(![]() ﹣
﹣![]() ),可求AB=
),可求AB=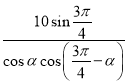 ,又
,又![]() ,结合
,结合![]() ,可得cos
,可得cos![]() ,可求两出入口之间距离的最小值为20(
,可求两出入口之间距离的最小值为20(![]() ).
).
(2)设切点为F,以![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线为
所在的直线为![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,设直线AB的方程为y=kx+t(k>0),可求t=20k,或t=60k,可求A(﹣20,0),此时OA=20,又由(1)可知当
,设直线AB的方程为y=kx+t(k>0),可求t=20k,或t=60k,可求A(﹣20,0),此时OA=20,又由(1)可知当![]() 时,OA=10
时,OA=10![]() ,综上即可得解.
,综上即可得解.
(1)过![]() 作直线OE⊥AB于E,则OE=10,设∠EOA=α,则∠EOB=
作直线OE⊥AB于E,则OE=10,设∠EOA=α,则∠EOB=![]() ﹣α,(
﹣α,(![]() ),
),
故AE=10tan![]() ,BE=10tan(
,BE=10tan(![]() ﹣
﹣![]() ),
),
AB=10tan![]() +10tan(
+10tan(![]() ﹣
﹣![]() )=10(
)=10(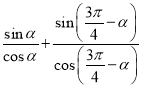 )=
)=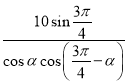 ,
,
又cos![]() =cos
=cos![]() (﹣
(﹣![]() cos
cos![]() +
+![]() sin
sin![]() )=
)=![]()
由![]() ,可得:2
,可得:2![]() ﹣
﹣![]() ,
,
故cos![]() ,当且仅当2
,当且仅当2![]() ﹣
﹣![]() ,即
,即![]() =
=![]() 时取等号,
时取等号,
此时,AB有最小值为20(![]() ),即两出入口之间距离的最小值为20(
),即两出入口之间距离的最小值为20(![]() ).
).
(2)由题意可知直线AB是以![]() 为圆心,10为半径的圆
为圆心,10为半径的圆![]() 的切线,根据题意,直线AB与圆C要相离,其临界位置为直线AB与圆C相切,
的切线,根据题意,直线AB与圆C要相离,其临界位置为直线AB与圆C相切,
设切点为F,此时直线AB为圆![]() 与圆
与圆![]() 的公切线,因为,出入口A在古建筑群和市中心
的公切线,因为,出入口A在古建筑群和市中心![]() 之间,
之间,
如图所示,以![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线为
所在的直线为![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,
,
由CF=5,OE=10,因为圆![]() 的方程为x2+y2=100,圆
的方程为x2+y2=100,圆![]() 的方程为(x+30)2+y2=25,
的方程为(x+30)2+y2=25,
设直线AB的方程为y=kx+t(k>0),
则: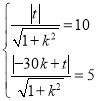 ,所以两式相除可得:
,所以两式相除可得:![]() =2,所以t=20k,或t=60k,
=2,所以t=20k,或t=60k,
所以,此时A(﹣20,0)或A(﹣60,0)(舍去),此时OA=20,
又由(1)可知当![]() 时,OA=10
时,OA=10![]() ,综上,OA
,综上,OA![]() .
.
即设计出入口A离市中心![]() 的距离在10
的距离在10![]() km到20km之间时,才能使高架道路及其延伸段不经过保护区.
km到20km之间时,才能使高架道路及其延伸段不经过保护区.


科目:高中数学 来源: 题型:
【题目】(本题满分12分)
今年十一黄金周,记者通过随机询问某景区110名游客对景区的服务是否满意,得到如下的列联表:
性别与对景区的服务是否满意 单位:名
男 | 女 | 总计 | |
满意 | 50 | 30 | 80 |
不满意 | 10 | 20 | 30 |
总计 | 60 | 50 | 110 |
(1)从这50名女游客中按对景区的服务是否满意采取分层抽样,抽取一个容量为5的样本,问样本中满意与不满意的女游客各有多少名?
(2)从(1)中的5名女游客样本中随机选取两名作深度访谈,求选到满意与不满意的女游客各一名的概率;
(3)根据以上列联表,问有多大把握认为“游客性别与对景区的服务满意”有关
注:![]()
临界值表:
P( | 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C经过M(1,3),N(4,2),P(1,﹣7)三点,且直线l:x+ay﹣1=0(a![]() R)是圆C的一条对称轴,过点A(﹣6,a) 作圆C的一条切线,切点为B,则线段AB的长度为_______.
R)是圆C的一条对称轴,过点A(﹣6,a) 作圆C的一条切线,切点为B,则线段AB的长度为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点
的焦点![]() 作直线交抛物线于
作直线交抛物线于![]() 两点,已知点
两点,已知点![]() ,
,![]() 为坐标原点.若
为坐标原点.若![]() 的最小值为3.
的最小值为3.
(1)求抛物线的方程;
(2)过点![]() 作直线
作直线![]() ,交抛物线于
,交抛物线于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 和点
和点![]() ,直线
,直线![]() ,
,![]() 的斜率乘积为常数
的斜率乘积为常数![]() ,设点
,设点![]() 的轨迹为
的轨迹为![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.存在非零常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() ,
,![]() 距离之和为定值
距离之和为定值
B.存在非零常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() ,
,![]() 距离之和为定值
距离之和为定值
C.不存在非零常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() ,
,![]() 距离之差的绝对值为定值
距离之差的绝对值为定值
D.不存在非零常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() ,
,![]() 距离之差的绝对值为定值
距离之差的绝对值为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+lnx(a∈R),g(x)=x2emx(m∈R,e为自然对数的底数).
(1)讨论函数f(x)的单调性及最值;
(2)若a>0,且对x1,x2∈[0,2],f(x1+1)≥g(x2)+a﹣1恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全国第五个“扶贫日”到来之前,某省开展“精准扶贫,携手同行”的主题活动,某贫困县调查基层干部走访贫困户数量.甲镇有基层干部60人,乙镇有基层干部60人,丙镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从甲、乙、丙三镇共选20名基层干部,统计他们走访贫困户的数量,并将走访数量分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 5组,绘制成如图所示的频率分布直方图.
5组,绘制成如图所示的频率分布直方图.
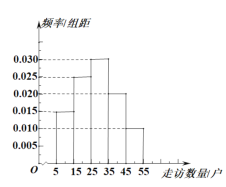
(1)求这20人中有多少人来自丙镇,并估计甲、乙、丙三镇的基层干部走访贫困户户数的中位数(精确到整数位);
(2)如果把走访贫困户达到或超过35户视为工作出色,求选出的20名基层干部中工作出色的人数,并从中选2人做交流发言,求这2人中至少有一人走访的贫困户在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com