
【题目】为了保护环境,2015年合肥市胜利工厂在市政府的大力支持下,进行技术改进:把二氧化碳转化为某种化工产品,经测算,该处理成本![]() (万元)与处理量
(万元)与处理量![]() (吨)之间的函数关系可近似地表示为:
(吨)之间的函数关系可近似地表示为: 且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
(1)当![]() 时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损?
时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损?
(2)当处理量为多少吨时,每吨的平均处理成本最少?
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() ,
,![]() 是椭圆上一点, 记直线
是椭圆上一点, 记直线![]() 、
、![]() 的斜率为
的斜率为![]() 、
、![]() ,且有
,且有![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点, 以
两点, 以![]() 、
、![]() 为直径的圆经过原点, 且线段
为直径的圆经过原点, 且线段![]() 的垂直平分线在
的垂直平分线在![]() 轴上的截距为
轴上的截距为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2009年推出一种新型家用轿车,购买时费用为![]() 万元,每年应交付保险费、养路费及汽油费共
万元,每年应交付保险费、养路费及汽油费共![]() 万元,汽车的维修费为:第一年无维修费用,第二年为
万元,汽车的维修费为:第一年无维修费用,第二年为![]() 万元,从第三年起,每年的维修费均比上一年增加
万元,从第三年起,每年的维修费均比上一年增加![]() 万元.(1)设该辆轿车使用
万元.(1)设该辆轿车使用![]() 年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为
年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为![]() ,求
,求![]() 的表达式;(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
的表达式;(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在汶川大地震后对唐家山堰塞湖的抢险过程中,武警官兵准备用射击的方法引爆从湖坝上游漂流而下的一个巨大的汽油罐.已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆.每次射击是相互独立的,且命中的概率都是![]() .
.
(1)求油罐被引爆的概率;
(2)如果引爆或子弹打光则停止射击,设射击次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() .( 结果用分数表示)
.( 结果用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,已知
,已知![]() .
.
(1)求椭圆的离心率;
(2)设![]() 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,经过原点
,经过原点![]() 的直线
的直线![]() 与该圆相切,求直线
与该圆相切,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校为了了解高一新生男生得到体能状况,从高一新生中抽取若干名男生进行铅球测试,把所得数据(精确到0.1米)进行整理后,分成6组画出频率分布直方图的一部分(如下图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
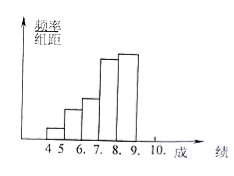
(1)请将频率分布直方图补充完整;
(2)该校参加这次铅球测试的男生有多少人?
(3)若成绩在8.0米以上(含8.0米)的为合格,试求这次铅球测试的成绩的合格率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com