
分析 (1)直线kx-y-4k+3=0,即 k(x-4)-y+3=0,可得直线l经过定点M(4,3);
(2)点M在圆C的内部,可得直线l和圆C总相交.
(3)当直线CM和直线l垂直时,弦长最短,再利用弦长公式求得最短弦长.
解答 (1)证明:直线kx-y-4k+3=0,即 k(x-4)-y+3=0,
∴直线l恒过定点,定点M(4,3);
(2)解:圆C:x2+y2-6x-8y+21=0,即(x-3)2+(y-4)2=4,表示以C(3,4)为圆心、半径等于2的圆.
而由CM=<2,可得点M在圆C的内部,故直线l和圆C总相交.
(3)解:由题意可得,当直线CM和直线l垂直时,弦长最短,最短弦长为2=2.
此时kCM==-1,∴k=1.
点评 本题主要考查圆的标准方程,直线经过定点问题,直线和圆的位置关系,弦长公式的应用,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
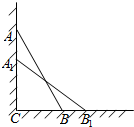 如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且米,则①BB1=-1米;②木棒AB的中点D所经过的路程为米.
如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且米,则①BB1=-1米;②木棒AB的中点D所经过的路程为米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
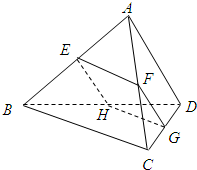 如图,空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,截面EGFH的最大面积是.
如图,空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,截面EGFH的最大面积是.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com