解:(Ⅰ)因为f(-1)=0,所以a-b+1=0.(1分)
因为方程f(x)=0有且只有一个根,所以△=b
2-4a=0.
所以b
2-4(b-1)=0.即b=2,a=1.(3分)
所以f(x)=(x+1)
2.(4分)
(Ⅱ)因为g(x)=f(x)-kx=x
2+2x+1-kx=x
2-(k-2)x+1
=
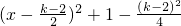
.(6分)
所以当
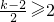
或
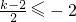
时,
即k≥6或k≤-2时,g(x)是单调函数.(9分)
(Ⅲ)f(x)为偶函数,所以b=0.所以f(x)=ax
2+1.
所以
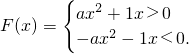
(10分)
因为mn<0,不妨设m>0,则n<0.
又因为m+n>0,所以m>-n>0.
所以|m|>|-n|.(12分)
此时F(m)+F(n)=f(m)-f(n)=am
2+1-an
2-1=a(m
2-n
2)>0.
所以F(m)+F(n)>0.(14分)
分析:(Ⅰ)根据f(-1)=0,可得a-b+1=0,再根据方程f(x)=0有且只有一个根,利用根的判别式再列出一个a和b的关系式,联立方程组即可解得a和b的值.
(Ⅱ)首先求出g(x)的函数关系式,然后根据函数的单调性进行解答,即可求出k的取值范围.
(Ⅲ)由f(x)为偶函数,求出b=0,设m>0,则n<0,又知m+n>0,故可得m>-n>0,最后把m和n代入求出F(m)+F(n)>0.
点评:本题主要考查函数解析式的求法、函数单调性的性质和奇偶性与单调性综合运用的知识点,解答本题的关键是熟练掌握函数单调性的性质,利用奇偶性进行解题,此题难度不是很大.

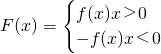 当mn<0,m+n>0,a>0,且函数f(x)为偶函数时,试判断F(m)+F(n)能否大于0?
当mn<0,m+n>0,a>0,且函数f(x)为偶函数时,试判断F(m)+F(n)能否大于0?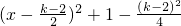 .(6分)
.(6分)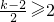 或
或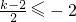 时,
时,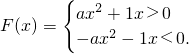 (10分)
(10分)
